太陽と地球
地上から地球の運動を見れば、地球は静止しています。
地球全体を見れば、地軸を軸に自転しています。
太陽を中心にして見れば円軌道を描いて公転しています。
さらには、宇宙は膨張しつづけているため、太陽系は静止していません。離れて見れば公転する地球は螺旋の動きをしています。
視点を変えれば、同じ現象も異なる動きを見せます。
では物体の運動を観察するとき、どこの視点を基準にすれば良いのでしょうか?
絶対空間
ニュートンはニュートン力学を構築する時、「絶対空間」という、物体が静止していることの基準となる空間がどこかに存在するということを仮定しました。
しかしアインシュタインは、物体の運動は相対的に観察されるもので「絶対空間は存在しない(認知できない)」と考え、相対性理論を発表しました。
系と座標系
系とは、同じ物理法則が働く空間を表します。
座標系とは観測者の視点を置く、静止した空間のことです。
等加速度運動する座標系
観測者Aは電車の外側、観測者Bは加速中の電車の中にいて、観測者はどちらも同じ球を持っています。

それでは、観測者Bが持つ赤い球の運動について見てみます。
観測者Aの座標系
観測者Aの座標系から見た赤い球は、糸に引っ張られて右方向に加速しているように見えます。

観測者Bの座標系
一方、観測者Bの座標系から見た赤い球は左に引っ張り続けられているように見えます。
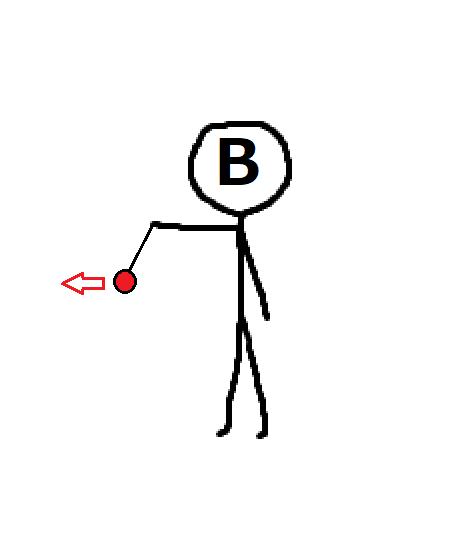
このように観測者の座標系によって物体の運動は異なります。
慣性系と非慣性系
座標系は、慣性の法則が成り立つ系(慣性系)とそうでない系(非慣性系)に分けられます。
慣性の法則
慣性系では、物体に外部から力が働かない(またはその合力が0である)とき、静止している物体は静止し続け、運動している物体はそのまま等速直線運動を続けます。
また、運動方程式は慣性系でしか成り立ちません。
運動法則は慣性系でしか成り立たない
今度は球を足元に置いて、外力が働いていない状態を考えます。

観測者Aの座標系では、球は外力を受けていない状態では静止しているため、慣性系にいることが分かります。

一方、観測者Bのいる電車の中は加速度運動をしています。
観測者Bの座標系で、球は外力を受けていない状態にもかかわらず左に転がっていくため、非慣性系にいることが分かります。

そのため、観測者Bの座標系(非慣性系)は観測者Aの座標系(慣性系)と同じ物理法則が成り立ちません。

慣性力という概念
非慣性系にある物体は慣性系と同じ物理法則が働きませんが、観測者Bの座標系には「みかけの外力(慣性力)がかかっている」と考えることで、慣性系と同じ系として見ることができ、運動方程式を成り立たせることができます。

重力と慣性力
重力場は非慣性系
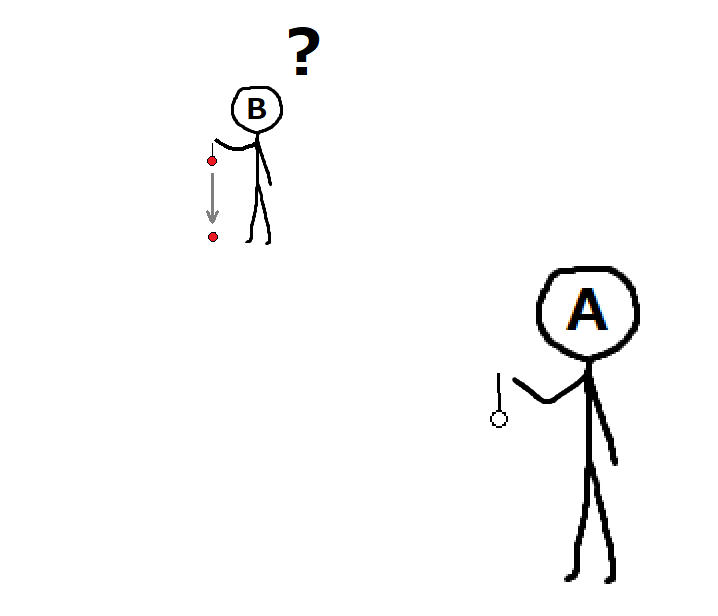
観測者Aは地上、観測者Bは宇宙空間にいて、観測者はどちらも同じ球を持っています。
この二人が手を静かに離した場合を考えます。
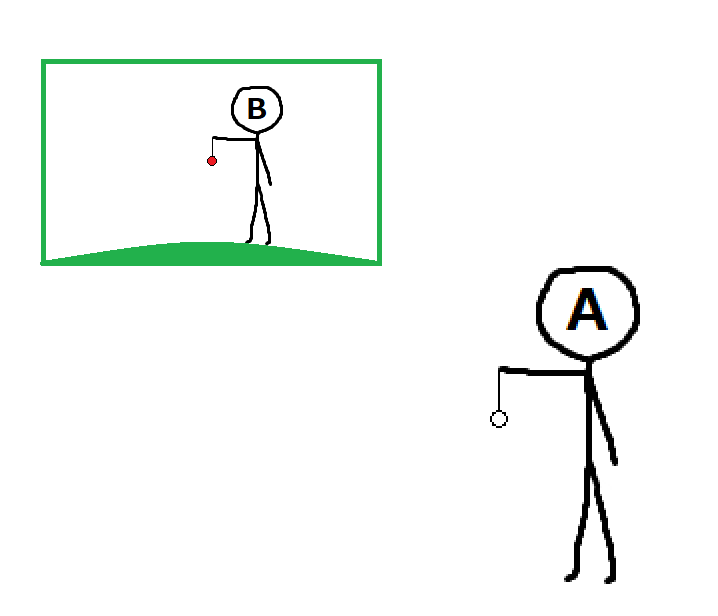
観測者Aの座標系では、球は外力を受けていない状態では空中に静止しているため、慣性系にいることが分かります。
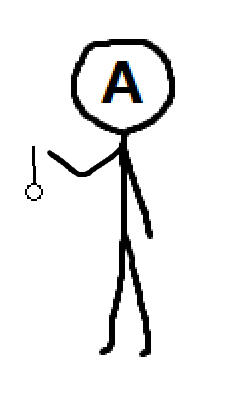
一方、観測者Bの座標系では、球は外力を受けていない状態にもかかわらず下向きに等加速度運動を始めるため、上下方向では非慣性系にいることが分かります。
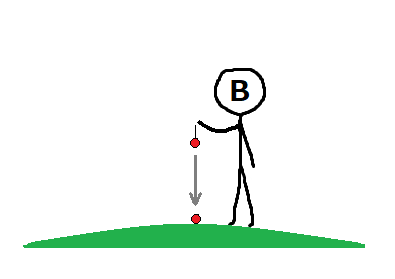
そのため、観測者Bの座標系(非慣性系)は観測者Aの座標系(慣性系)と同じ物理法則が成り立ちません。
そこで観測者Bの座標系には「みかけの外力がかかっている」と考えることで、慣性系と同じ系として見ることができ、運動方程式を成り立たせることができます。
そしてこの正体は重力です。

重力と慣性力は等価
重力を受けた物体は、質量によらず全く同じように自由落下し、同時に着地します。
ガリレオ・ガリレイは、「物体の落下速度はその物体の重さによらない」ということを証明するために、ピサの斜塔から大小二つの鉛の玉を同時に落とし「大小両方の玉が同時に地面に落下することを確認しました。

無重力の空間に「上向き」に加速度g(重力と同じ大きさ)で加速上昇するエレベーターを考えてみます。
エレベーターの中の観察者は、慣性力によって「下向き」の力を感じます。ここで、同じ高さから二つの物体を同時に静かに離すと、二つの物体には慣性力が生じて下方向へ進み、同時に床に着きます。
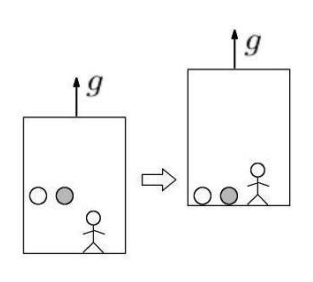
これは外の観察者から見れば、床の方が物体に近づいて行くように見えますが、中の観察者から見れば、これは重力加速度gの地上にいるのと物理的に全く同じであり、区別が付きません。
アインシュタインは、慣性力は重力の性質と同じであると考えました(アインシュタインの等価原理)。
そして、重力場にある座標系を加速度運動する座標系として考えることで、慣性系でしか適応できなかった特殊相対性理論を、非慣性系の座標系でも適応できるようにしました。これが一般相対性理論と呼ばれます。


コメント