ド・ブロイ波
アインシュタインの光量子仮説では、光は波動性だけでなく、粒子性も持ち合わせているとされました。
これに関してフランスの物理学者のルイ・ド・ブロイは、逆に電子などの物質(粒子)も、粒子性だけでなく波動性があるのではないかという仮説を立てました。
この波はド・ブロイ波(物質波)と呼ばれ、その波長をド・ブロイ波長といいます。
ド・ブロイの仮説は電子線回折の実験などで支持され、ド・ブロイ波の発見は現在の量子力学の基礎であるシュレディンガー方程式に繋がっています。
導出
まず、光子の運動量は次の式で表されます。
$$ p=\frac{E}{c}=\frac{hν}{c}=\frac{h}{λ} $$
h:プランク定数
λ:波長
また、物質(粒子)の運動量は次の式で表されます。
$$ p=mv $$
m:質量
v:速度
これより、ド・ブロイ波長(アインシュタインード・ブロイの関係)は次の式で表されます。
$$ λ=\frac{h}{p}=\frac{h}{mv} $$
電子の波動性に関して、最も主流の解釈はコペンハーゲン解釈で、一つの電子は複数の場所に同時に存在し、電子が発見されると位置が確定すると言われています。
ド・ブロイ波はその発見しやすさを波動の式として表していると考えられています。
ボーアの原子模型
ラザフォードの原子模型において原子核の周囲を電子が回っていると仮定した場合、古典電磁気学の法則によれば、電子はただちに電磁波を放射し、原子核に引き寄せられるため、原子は安定して存在できないことになります。
その矛盾から、どのようなメカニズムが電子を安定させているかが物理学の大きな問題でした。
そこでボーアは、ド・ブロイ波長λの自然数倍を満たす軌道上に電子がある(電子の波が軌道上で定常波を作る)ときのみ安定するというボーアの原子模型を考えました。
ボーアの量子条件
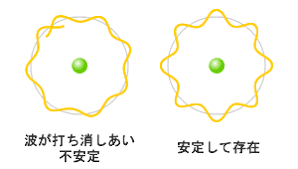
原子軌道は円運動をしており、電子は円軌道上を等速円運動すると仮定した上で、その円周は次の式で表されます。
$$ 2πr_n=λn \quad(n=1,2,3・・・) $$
より
$$ 2πr_n=\frac{h}{mv} n \quad(n=1,2,3・・・) $$
電子が別の軌道に移るときは、エネルギー準位の差と同じエネルギーを与えられるか放出しなければならないことが分かります。
これは、「原子はなぜ特定の波長の電磁波だけを放出したり吸収したりするのか」という疑問をうまく説明するものでした。
円軌道半径
クーロン力
電子は原点に静止している陽子の周りをクーロン引力で引っぱられながら運動します。
$$ F=\frac{1}{4πε_0}・\frac{Ze^2}{r^2} $$
このとき、遠心力(=向心力)とクーロン力との釣り合いは力学の式で次のように表されます。
$$ m\frac{v^2}{r_n}=\frac{1}{4πε_0}・\frac{Ze^2}{r^2} $$
陽子の電荷はZe、電子の電荷はe。
円軌道半径
量子条件の式より、
$$ v=\frac{h}{2πmr}n $$
と変形し、これを運動方程式に代入するとn番目の円軌道半径rnが
$$ r=\frac{ε_0h^2}{πmZe^2}n^2 \quad(n=1,2,3・・・) $$
で表されます。
ボーア半径
水素原子(陽子数Z=1)の電子の基底状態(主量子数n=1)での軌道半径は最小となり、ボーア半径と呼ばれます。
$$ r_1=\frac{ε_0 h^2}{π m e^2}$$
n番目の円軌道上の電子の全エネルギー
ボーア模型で、エネルギー準位の高低を決めているものは電子と考えることができます。
電子が半径の一番小さい軌道を回っている状態を基底状態といいます。
量子数nが大きくなり、電子が半径の大きい軌道を回る状態を、励起状態といいます。
さらに、イオン化エネルギー以上のエネルギーを電子が受け取ると、電子が原子から飛び出し、イオン化状態となります。
運動エネルギーT
$$ T=\frac{1}{2} mv^2 $$
ポテンシャルエネルギーU
$$ U= – \frac{Ze^2}{4 π ε_0 r} $$
全エネルギーE
$$ E=T+U= \frac{1}{2} mv^2 – \frac{Ze^2}{4 π ε_0 r} $$
これと量子条件の式より
$$ E_n = – \frac{m Z^2 e^4}{8 ε _0 h^2}・\frac{1}{n^2} \quad(n=1,2,3・・・) $$
量子数nの値によって飛び飛びの値をもつエネルギーEnをエネルギー準位といいます。


コメント