エネルギー損失
荷電粒子が物質中を通過する際、物質との相互作用によってエネルギーを失います。
荷電粒子が物質内を通過するとき、経路に沿って標的物質の原子を電離(イオンと電子の対が生まれる)しながら次第にエネルギーを失い、最後に停止します。
荷電粒子が物質との相互作用でエネルギーを失う過程には以下の2通りがあります。
衝突損失:質量が大きい粒子(α線など)は進行方向の軌道電子と衝突して弾き、電離と励起をすることによりエネルギーを失っていきます。
放射損失:質量の小さい荷電粒子(β線など)の場合は電場に軌道を曲げられて減速し、制動X線を放出する(制動輻射)ことによりエネルギーを失います。

比電離
荷電粒子が物質中を通過するとき、飛跡の単位長さ当たりに発生させるイオン対の数です。
入射荷電粒子がその飛跡上で直接起こす電離のことを一次電離といい、一次電離にのみ起因するイオン電子対の数は一次比電離といいますが、一般的には一次電離に際して放出された二次電子がつくる二次イオン対も含めた全イオン対に対する全比電離を言います。
ブラッグ曲線
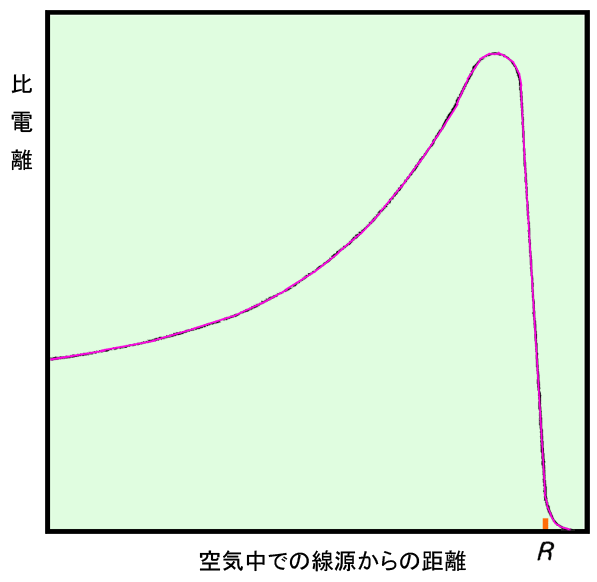
荷電粒子の進んだ距離と比電離の関係をプロットしたものをブラッグ曲線 (Bragg curve) と言います。
イオン粒子はエネルギーの減衰により速度が低下するにつれ、速度の2乗に比例して大きなクーロン力を受けやすくなり停止点(飛程)の直前で急激に相互作用を起こして減速します。このとき、大量の放射線を発生させます。


阻止能S [MeV/cm]
一般に比電離は阻止能に比例するため、阻止能に対する性質(ブラッグ曲線)は、そのまま比電離についても成立します。
阻止能S(Stopping Power)[MeV/cm]は、放射線が標的物質中を進むとき、厚み1[cm]あたりに荷電粒子が失うエネルギー[MeV]です。
厚みx[cm]まで進んだ放射線が失ったエネルギーをE(x)とすると、阻止能S(Stopping Power)は次の式で表されます。
$$ S=-\frac{dE}{dx} $$
①荷電粒子は物質中の電子にエネルギーを与え、励起や電離(電磁相互作用)を起こすことでエネルギーを失います。この現象による阻止能を衝突阻止能Scol(collisional)と呼びます。
②この現象による阻止能を放射阻止能Srad(radiative)と呼びます。重荷電粒子の制動放射は高いエネルギー領域でのみ起こると考え、その他のでは無視します。
阻止能S=衝突阻止能Scol+放射阻止能Srad
線阻止能
荷電粒子が物質中において衝突(電離または励起作用)によって単位長さ当たりに失うエネルギー (dE/dx)colをいう。 単位は、J/mまたはkeV/μmである。
阻止能を生ずる原因は、入射粒子と物質を構成する原子との間の弾性衝突と非弾性衝突とがある。一般に粒子のエネルギーが低い場合には弾性衝突が支配的で、入射エネルギーが高い場合には非弾性衝突が支配的である。阻止能は物質中での飛程を決めるだけではなく、粒子からのエネルギー付与の空間分布を決める重要な量である。阻止能の測定法には、薄膜を通過する間での粒子のエネルギー損失の測定、薄膜に吸収されたエネルギーの測定、ドップラー効果を利用する方法などがある。
LET(線エネルギー付与)=線衝突阻止能
LET(線エネルギー付与/Linear energy transfer)は、放射線の性質の1つを表現するもので、荷電粒子が通過する過程で、単位長さの飛跡の聞に電離現象などを介して介在物質に与えるエネルギーの大きさをいう。
すなわち、荷電粒子の飛跡に沿った単位長さあたりのエネルギー損失率[keV/μm]
電子的阻止能
電子的阻止能(electronic stopping power)とは、媒質中を移動するイオンが媒質の束縛電子との非弾性衝突によって減速される効果を表す。
「非弾性」という用語は衝突の過程で運動エネルギーが失われることを示している(失われたエネルギーは、媒質束縛電子とイオン電子雲の両者の励起に使われる)。
イオンが電子と衝突する回数は莫大なものであり、また媒質中を移動するイオンの荷電状態は常に変化しうるため、あらゆる可能な荷電状態についてあらゆる相互作用を考慮するのは非常に難しい。
そこで電子的阻止能を、異なる荷電状態に対するあらゆるエネルギー損失過程の平均を表す単純な関数 Fe(E) として扱うことが多い。
核子1個あたりのエネルギーが数百keVを超える領域では、数%の精度で関数 Fe(E) を理論的に決定することができる。
その理論的な枠組みはいくつかあるが、ベーテの式がもっともよく知られている。
荷電粒子の質量阻止能
下の図はミュー粒子(正電荷)の質量阻止能を表しています。
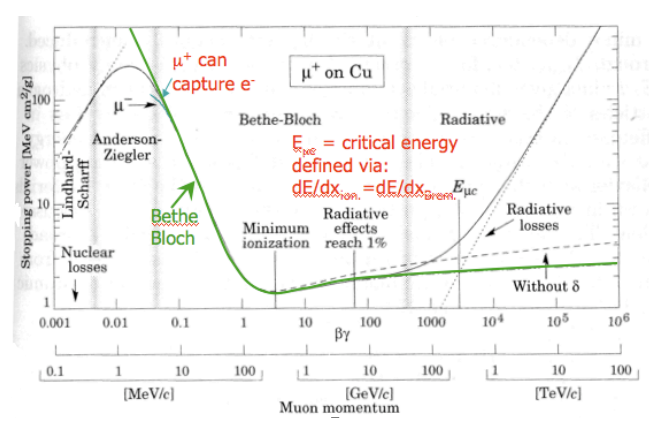
下の図は荷電粒子が低~中エネルギー領域での質量阻止能を概念的に表しています。

低エネルギー領域(A~B)

低エネルギーの荷電粒子は標的物質の電場によって減速され、速度が大きく減少するため、阻止能が急激に上昇します。
後述のベーテの式は適用されず、理論的取り扱いも不正確です。
エネルギーが100keVを下回る領域においては、電子的阻止能を解析的モデルによって決定することは困難。
荷電粒子の速度が標的物質の軌道電子の速度と同程度以下では、物質から電子を捕獲するようになります。
阻止能は荷電粒子のエネルギーや物質の原子番号だけでなく、低エネルギー域では後述のように物質の電子状態にも依存する。
α線のエネルギーが約40MeV以上(104MeV以下)では、阻止能はほぼそのエネルギーに反比例している。この領域での阻止能はベーテの式で与えられる。
α粒子のエネルギ ーが約104MeV以上になると制動放射によるエネル ギー損失が大きくなり、上式の対数の項に補正が必要となる。
以下にα粒子のエネルギ ーが低下するに従って起こる現象を説明する。
α粒子のエネルギーが40MeV以下になると、α粒子の速度は原子中の内殻電子の速度よりも小さくなり、それらを電離させることができなくなるため補正項(内殻補正)が必要となる。
α粒子のエネルギーが0.5~1MeVまで低下すると阻止能は最大となる。
この最大値はブラッグ曲線の最大値に対応している。
ここでは物質中の電子を捕獲するようになる。
He2++e–→He+
さ らに
He++e–→He
といった反応が起こり、電離に必要な有効電荷が減少する。
個々のα粒子の減速過程では、上式の逆反応で捕獲した電子を放出することもあり、実際には電子の捕 獲と放出とを多数回繰り返しながらエネルギ ーを失なう。
阻止能が最大値を過ぎてα粒子のエネルギーが低下すると、阻止能がα粒子のエネルギーに比例する領域になる。
さらに減速されると、α粒子と物質中の原子核との衝突の割合が増加する。
核的阻止能
核的阻止能(nuclear stopping power)とは入射イオンと原子核との弾性衝突によって減速される。
阻止能の大半は電子的阻止能であるが、停止直前の低エネルギーのイオンでは重要となる。
下の図はアルミニウムに入射したアルミニウムイオンに対する核的および電子的阻止能を示したもの。
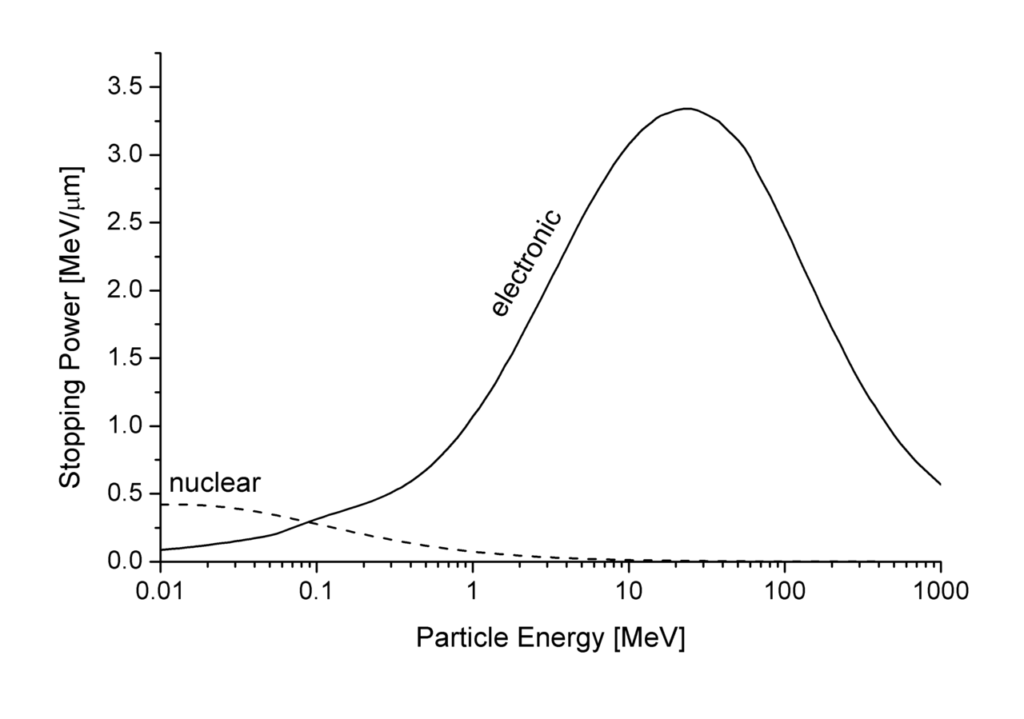
核的阻止能曲線は核子当たり1 keV程度のエネルギーで最大値を取るのが普通で、低エネルギー領域を除けば核的阻止は無視できる。
入射イオンの質量が増加すると核的阻止能も増加する。非常に軽いイオンが重い物質の中で減速する場合にはすべての領域で核的阻止が電子的阻止より弱くなる。
クーロン相互作用による荷電粒子間の弾性散乱をラザフォード散乱と呼びます。
α線が原子核との弾性散乱を行うと、α線は散乱され進行方向が変わる。
散乱される角度(θ)分布はラザフォー ドの散乱公式に示されているようにsin4(θ/2)に逆比例するので、小角度の散乱が多いことになる。
しかし、原子核の質量がα粒子よりも大きい場合には、散乱によってα粒子が跳ね返される確率もある。
これを後方散乱といい,後 で述べる ように元素分布 の測定 に利用 されてい る。
また線源や検出器周辺でも散乱され、エネルギーの低下したα線が観測されることになる。
反跳された原子核は、一般に電離には寄与しないので、電離量からエネルギーを測定する検出器では、この分だけエネルギーが低く観測されることになる。
しかし、α線の場合は実用上無視できる程度である。
物質が結晶の場合には、原子核が反跳されることによって結晶欠陥が作られる。
これは放射線損傷と呼ばれており、Si検出器を強いα線で照射したときに起こる特性劣化の原因となって いる。
なお、低エネルギー域での阻止能の理論的な取扱いにはLSS理論がある。
イオンのエネルギーのほとんどは標的電子に付与され、標的原子核へ与えられるエネルギーはごくわずかである。
しかし、イオンは減速されると荷数が減って電気的中性に近づくため、標的電子との相互作用によるエネルギー損失は小さくなる。
その結果、イオンは原子核と弾性衝突を繰り返すことで、その運動エネルギーを標的原子核へ与えることになる。
低速イオンと標的原子核の衝突では核間距離が大きくなることから、原子核のクーロンポテンシャルが核外電子に遮蔽される影響を考慮する必要がある。
LindhardらはThomas-Fermi模型を用いて電子状態を記述することでイオンのエネルギー損失に関する統一的な理論を構築しており一般に受け入れられている。
比較的低エネルギー(核子あたり数MeV以下)の遅いイオンでは、標的原子核との相互作用の割合が高くなる。
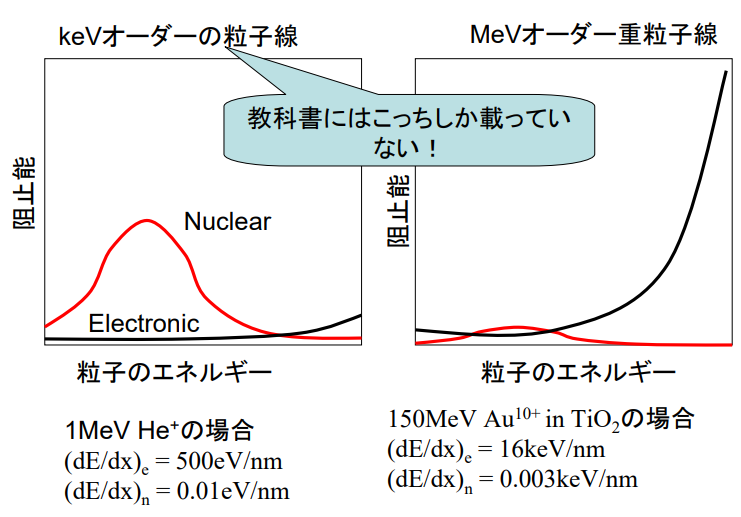
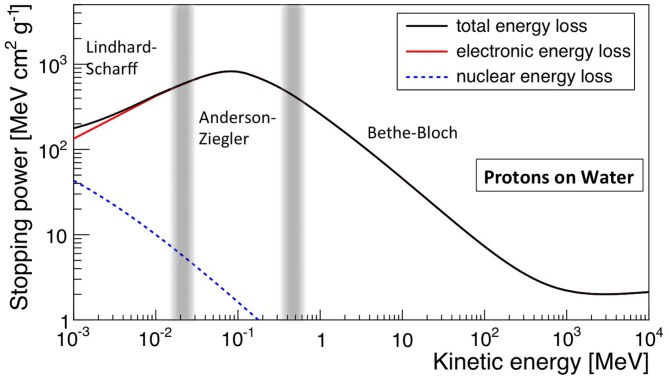
中エネルギー領域(B~D)
荷電粒子の衝突阻止能はベーテの式(Bethe-Bloch fomula)で与えられています。
ベーテの式は荷電粒子の速度が十分大きいという仮定に基づいているため、中程度のエネルギーで合致します。
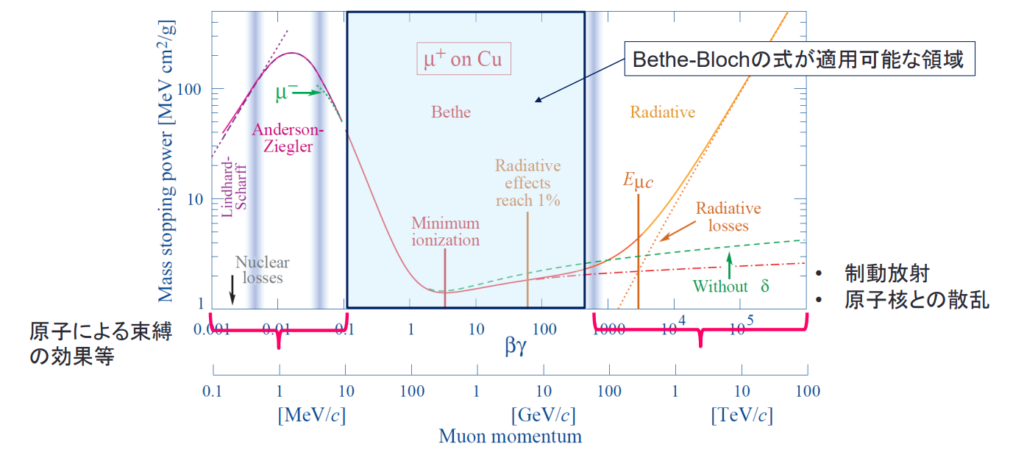
B~Cの範囲では、物質中の電子や原子核との衝突が多様化し減速しにくくなるため、阻止能が1/v2に比例して急速に減少します。
Cのエネルギー損失が最少になる領域での値を最小電離(Minimum Ionization)と呼びます。
C~Dの範囲では[ ]の項(ストッピング数)が実効的になり、阻止能は緩やかな上昇を示します。
一般的に、荷電粒子のエネルギーが1MeVを超えると、物質中を通過する際の衝突阻止能の上昇は緩やかになります。

高エネルギー領域(D~)
高エネルギー領域では放射損失や原子核との散乱によって、より多くのエネルギーを失うため、阻止能は上昇します。
イオンのエネルギーが非常に高いときには[3]、物質中の電界を通過することで発生する制動放射による放射阻止能も考慮しなければならない[13](全阻止能から放射阻止能を引いた部分は衝突阻止能と呼ばれる)。飛来粒子が電子である場合は常に放射阻止能が重要となる。イオンエネルギーが大きい場合、核反応によるエネルギー損失も起こりうるが、通常そのような過程は阻止能としては考えられない[13]。
ベーテの式
ベーテの式(Bethe-Bloch fomula)は以下の通りです。
$$ S=n・\frac{z^2}{β^2}・\left( \frac{e^2}{4πε_0} \right)^2 \frac{1}{mv^2} \left[ \log_e \left( \frac{2mv^2}{I(1-β^2)} \right)-β^2 \right] $$
z: 荷電粒子の原子番号
v: 荷電粒子の速さ
I:物質の平均励起エネルギー
$$ β=\frac{v}{c} $$
v: 荷電粒子の速度
c: 光速度
$$ n=\frac{ρ}{A}N_A Z $$
n: 電子密度
ρ: 標的物質の密度
A: 標的物質の質量数
NA: アボガドロ数
Z: 標的物質の原子番号
ここで重要な部分は
$$ S ∝ n・\frac{z^2}{β^2} $$
で、\( β=\frac{v}{c} \) より
$$ S ∝ n・\frac{z^2}{v^2} $$
荷電粒子の阻止能は主に
①入射する放射線の電荷の2乗に比例し、入射速度の2乗に反比例します。
②標的物質の電子密度に比例します。
また、入射する荷電粒子のエネルギーと阻止能の比例関係も導出できます。
$$ E=\frac{1}{2}mv^2 $$
より
$$ v^2=\frac{2E}{m} $$
なので
$$ S ∝ n・\frac{z^2}{v^2} = n・\frac{2mz^2}{E} $$
となり
$$ S ∝ n・\frac{mz^2}{E} $$
が導出できます。

ブラッグ曲線
電子以外の荷電粒子(陽子、α、その他重荷電粒子)は質量が電子に比べてはるかに重いため、電子との衝突によりほとんど曲げられず、散乱によるエネルギー損失は少ないです。
重荷電粒子は速度の2乗に反比例して大きな抵抗を受けるため、速度が遅くなってくると、急激にエネルギーを失います。
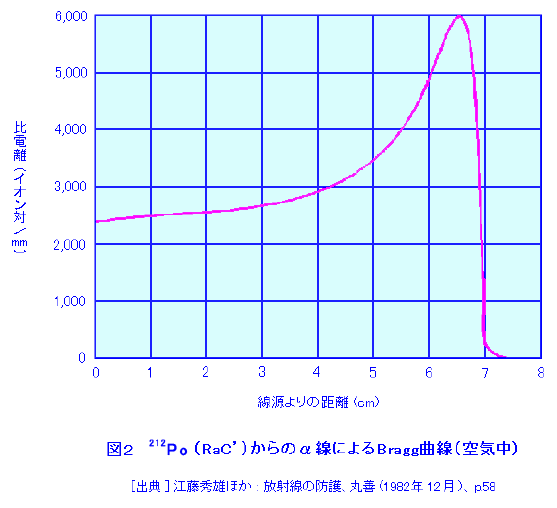
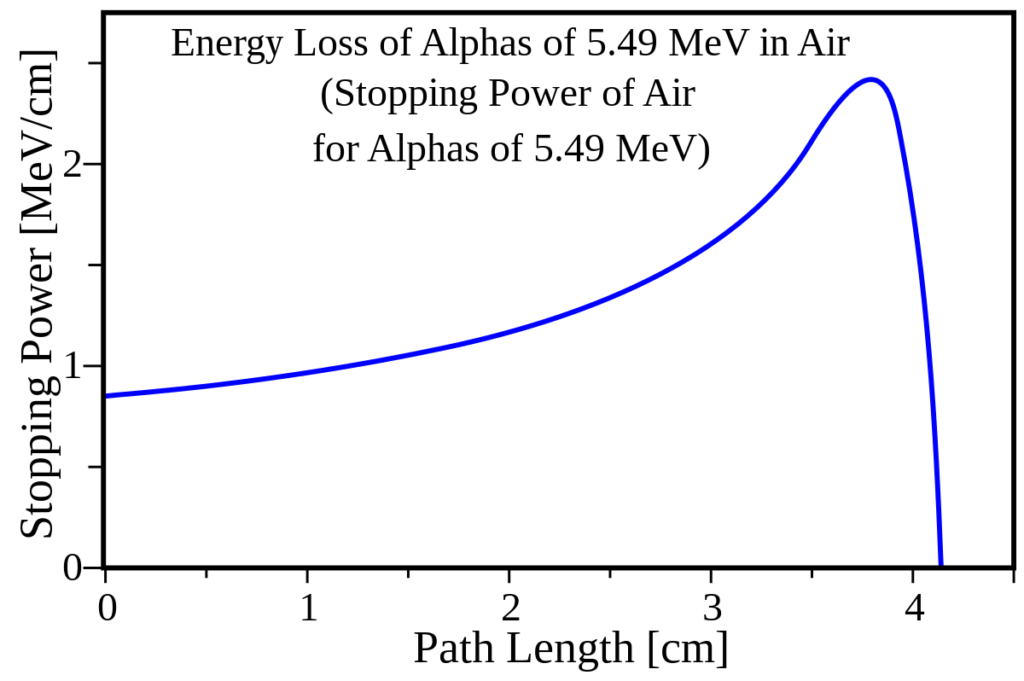
下の図は荷電粒子(α線:E=5.49[MeV])が標的物質内(空気)で進んだ距離に対する阻止能(ブラッグ曲線)を表しています。
阻止能は飛程(粒子が停止するまでに飛ぶ距離)に近づくにつれて増加し、最大値(ブラッグピーク)に達した直後にゼロとなります。
飛程
物質中の電子との衝突によって、簡単に方向やエネルギーが変化するため、まっすぐに進まず、広い範囲に広がります。
ある荷電粒子における飛程の最大値は標的物質の種類によらず、同じぐらいの値になることが知られています。
最大飛程(Range)は次の式で表されます。
$$ R= \int^{0}_{E_0}\frac{dx}{dE}dE $$
この式の意味について考えていきます。
仮に、阻止能が一定であればイメージしやすいのですが、荷電粒子の持つエネルギー(これが変動する)によって阻止能(失うエネルギーに対する進んだ距離)が変化するので、積分計算が必要になってきます。
まず、積分の考え方についてです。
$$ E= \int^{x}_{0} \frac{dE}{dx} dx $$
x軸上のある一点における距離(dx)のときの『阻止能』を、距離0~x[cm]まで積算するということです。
阻止能dE/dx:ある一点における距離(dx)のときの失うエネルギー(dE)
積算した結果は、荷電粒子が全経路長x[cm]の間に失ったエネルギーの総量になります。
ここで、阻止能が一定の場合を考えてみます。
となります。
次に阻止能の逆数について考えます。
阻止能Sは1[cm]進む間に失うエネルギー[MeV]の大きさ[MeV/cm]のことでした。
一方、阻止能の逆数1/Sはエネルギーを1[MeV]失う間に進んだ距離[cm/MeV]と考えられます。
例えば、どのエネルギーの大きさでも阻止能が2[MeV/cm]の場合、エネルギーを1[MeV]失うときに0.5[cm]進むと考えられます。入射エネルギーが10[MeV]の荷電粒子がすべてのエネルギーを失ったとき、その飛程は
$$ 10[MeV]×0.5[cm/MeV]=5[cm] $$
となります。
『エネルギーを10[MeV]使ったときに到達する距離』と考えられます。
この二点を踏まえて飛程の式を見てみます。
$$ R= \int^{0}_{E_0}\frac{dx}{dE}dE $$
ある一点におけるエネルギー(dE)のときの『1MeVあたりの距離』を、エネルギー0~Eまで積算するということです。
積算した結果は荷電粒子が進んだ距離の総量で、つまり最大飛程(到達した距離)です。
電子のAl中での最大飛程R
エネルギーE[MeV](1~10の範囲)の電子の飛程Rは入射エネルギーで決まり、おおよそ
\( 0.5E \) [cm]
となります。
α線の空気中での飛程R
\( 0.3E^{\frac{3}{2}} \) [cm]
α線のエネルギーは4-8MeV程度なので、空気中での飛程は数cmとなります。
α線のエネルギーが5Mevのとき、飛程は3.6cm
α線のエネルギーが6.3Mevのとき、飛程は5cm
電子線について
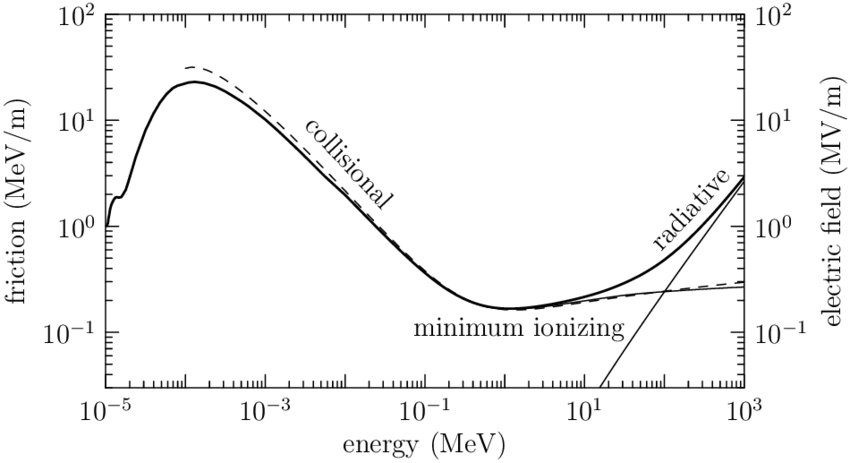
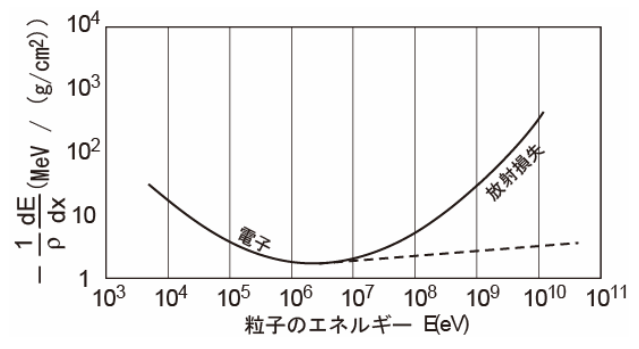
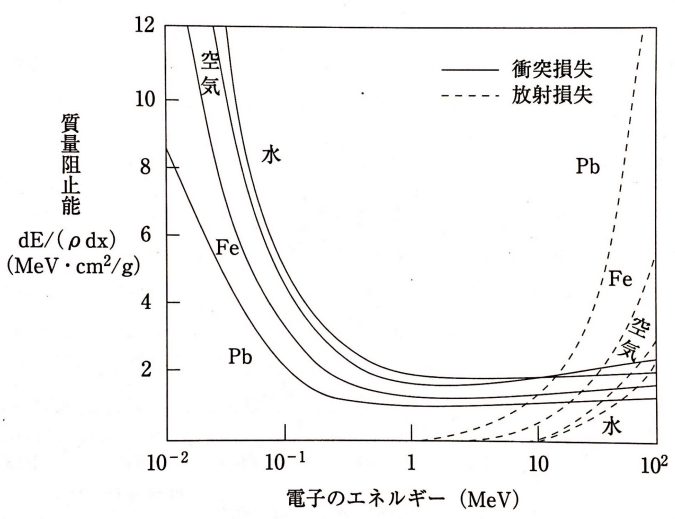
電子の衝突阻止能は、エネルギーが1MeVあたりで電子の速度はほぼ光速度に近づくため、それ以上のエネルギー領域ではほぼ一定となります。

阻止能比
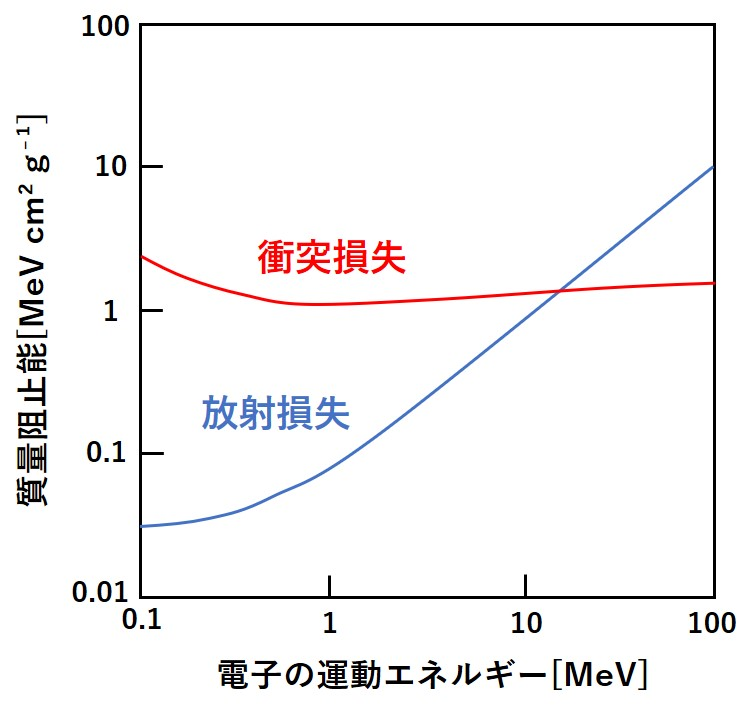
エネルギーの高い電子ほど、制動放射によるネルギー損失は大きくなります。
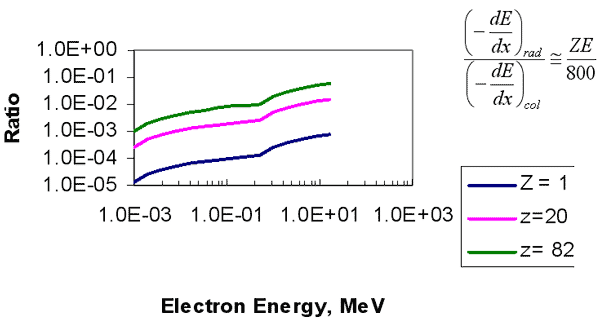
放射阻止能と衝突阻止能の比は、電子のエネルギーE を MeV で表すと、近似的に
$$ \frac{S_{rad}}{S_{col}} ≒ \frac{EZ}{800} $$
と表され、エネルギーの高い電子ほど制動放射の影響は大きくなる。
ただし、放射性核種から放出されるβ線では、そのエネルギーがせいぜい数 MeV のオーダーであるので、制動放射はあまり問題とならない。
制動放射が実際上重要になるのは、電子加速器等における遮蔽と制動 X 線の発生である。
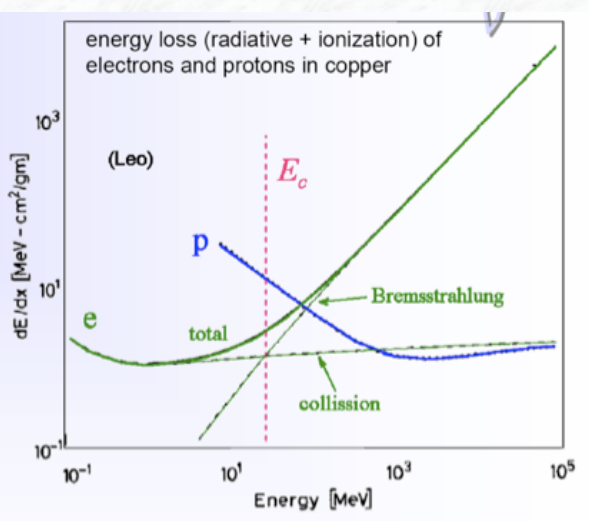
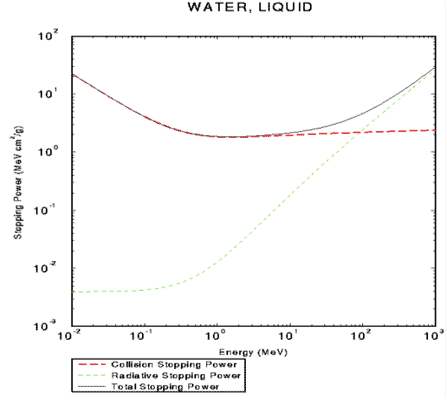
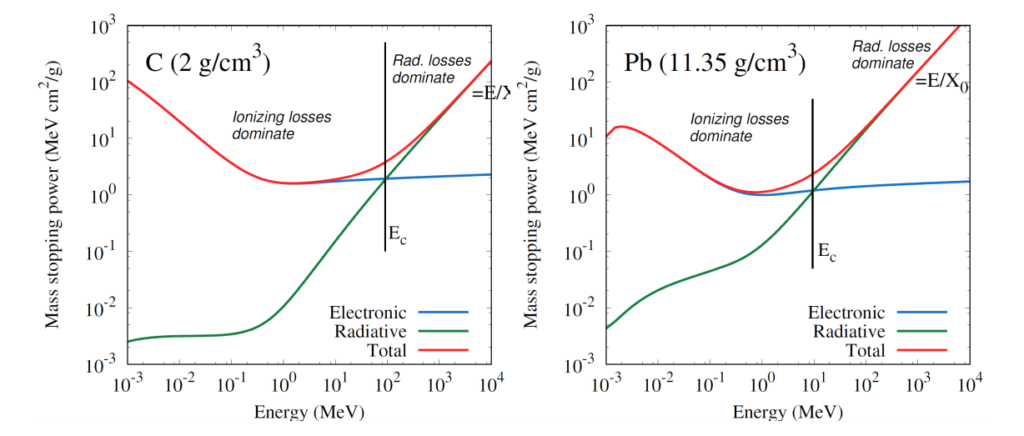
図 2.1 に空気中における電子の阻止能の変化をエネルギーの関数として示す。
先に述べたように、1MeV を超えるころから、衝突阻止能はほぼ一定となるが、放射阻止能が増加し始め、100MeV 以上では明らかに放射阻止能の寄与が大きくなる。


ブラッググレイの空洞原理
光子によって生成される二次電子の 飛程が検出器の空洞サイズよりも長い場合につい て、吸収線量を評価するために考えられた理論
阻止能と吸収線量(γ線)の間には、ある条件で
ブラッググレイの空洞原理が成立します。
ブラッグ・グレイの空洞原理とは、
γ線(X線)の、物質による吸収係数(Dm)と気体による吸収係数(Dg)の比は、
荷電粒子の、物質による平均質量阻止能(Sm,en)と気体の平均質量阻止能(Sg,en)の比と等しいことを示した原理です。
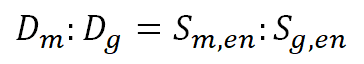
ブラッグ・グレイの空洞原理が成立する条件は、次の2点です。
・「電離箱の壁の厚さ」が2次粒子の飛程より十分に大きく、
入射放射線が乱されない程度に十分薄いこと。
・「空洞の大きさ」が、充填ガス中の2次粒子の飛程と比べて小さいこと。


コメント