http://lambda.phys.tohoku.ac.jp/~miwa9/3rd_exp/Appendix.pdf
放射線は物質を通過した時に減少するが、その減少の量:dIは入射光子の数:Iに比例し物質の量dxに比例すると考えるのが自然です。
比例定数をμ(cm-1)として式で書くとdI=-μIdx となる。
これは上の半減期の議論と同じで、 I(x)=I0 exp(-μx)です。
ここでμ=σnと書いて、σは長さの二乗(面積)の単位を持つので断面積と呼ばれます。
nは物質の単位体積あたりの数ですが、扱いやすさを考えてnとして密度、断面積としてcm2/gにすることがほとんどで、図3もその単位系になっています。
これはちょうど面積σを持った無数の標的をピストルで打った時に当たる確率を表しているようなものです。
荷電粒子の相互作用
制動放射
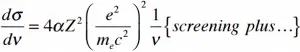
光子の相互作用
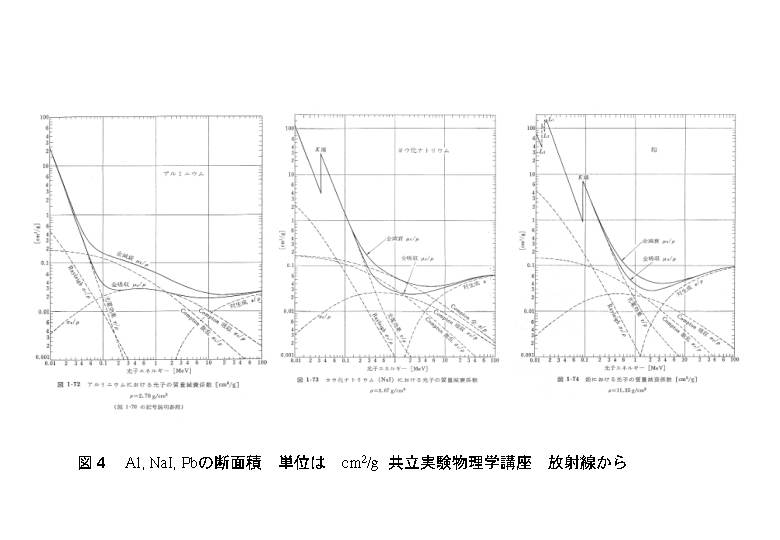
線減弱係数
単位光子フルエンスに対する電子 1 個あたりの相互作用の期待値は電子断面積と呼ばれる.
線減弱係数と電子断面積eσ(cm2)の関係は次式で表される.
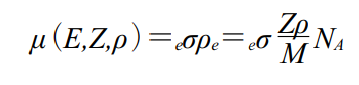
単元素物質の原子番号を Z,
原子量を M
密度を ρ(g・cm-3)
NA:アボガドロ定数
散乱
散乱とは入射放射線が視線方向から逸らされることになるのだが、散乱体として一番普通に考えられるのは電子です。電子の散乱断面積が基本となります。電子はまぎれも無く電磁相互作用ですから、電子の古典半径の二乗程度として散乱断面積が与えられることは容易に想像されます。
σt=(8/3)πre2= 8π/3(e2/mc2)= 6.65x 10-24 cm2
程度であり、この散乱断面積を特別にThomson散乱断面積と呼ぶ。
X線の物質のよる散乱には、光子のエネルギーに変化のない散乱と、変化の起こる散乱
があり、変化のない散乱を弾性散乱、変化のある散乱を非弾性散乱と呼ぶ。弾性散乱の代
表的な過程は Thomson 散乱と呼ばれる。非弾性の場合は Compton 散乱と呼ばれる。
光電効果
もっとも良く知られた光子と物質の反応が光電子吸収です。
光量子の発見はこの光電効果の性質からもたらされました。
今エネルギー hνを持った光子が物質に入射し、主にK殻の電子と作用して電離を行う。
Ee=hν-Iのエネルギーを持った電子が原子から飛び出る。
I は原子における電子の結合エネルギーであり、我々がここで考えているエネルギーに比べれば小さい。
入射エネルギーがIより小さければ、いかに放射線を強くしても光電効果は当然起こらない。これが光量子の発見を導きました。この光電効果の吸収の断面積は
σp = σtZ5/13724√2 (E/mc2)-7/2
で与えられる。特徴は原子番号zの5乗の依存性を持つことです。式から高いエネルギーと軽い物質では余り重要ではないことがわかります。
コンプトン効果
光子のエネルギーが電子の束縛エネルギーに比べて大きくなると、電子を自由電子とみなした衝突が支配的になります。
これをコンプトン散乱とよぶ。
入射エネルギーhνと散乱角と散乱電子、光子hν`の間にはエネルギー保存、運動量の保存がなりたちます。
角度の関係を図3のように定義します。
散乱電子のエネルギーをEsとすると、エネルギー保存から光子のエネルギーhν’はhν’= hν-Es 運動量の保存から
hν’= hν mc2/(mc2+(hν(1ーcosθ))
となる。
この時の全散乱角にわたって積分した散乱断面積はKlein-Nishinaの式として計算され,ε=E/mc2として、σc = zσt(1-2ε + 5.2ε2 -13.3ε3) で近似されます。
εが0の極限ではσtとなります(これらの証明を考えてみてください)。
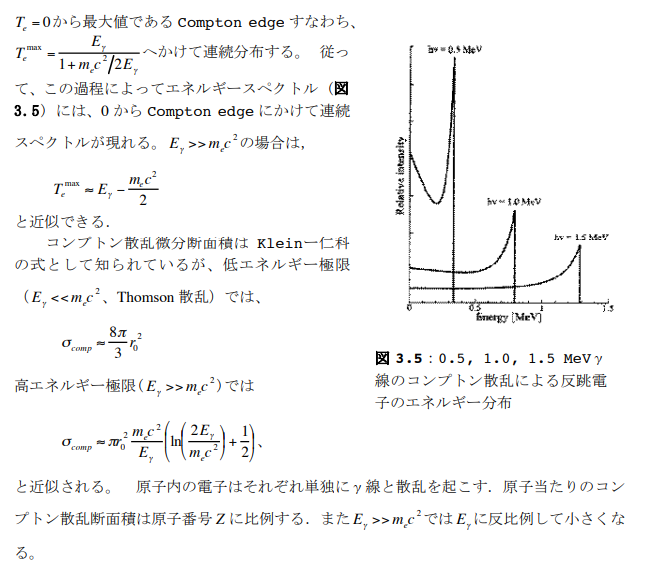
電子対生成
更にエネルギーが上がると、γ線でいるよりも電子、陽電子の対を作った方が安定になって来ます。電子の静止エネルギーは2mc2=1.02 MeVなので、このエネルギー以上で対生成が行われるようになります。しかしコンプトンに比べて対生成は10 MeV を越えるような大きなエネルギーにならないと支配的ではない。
光子に対する全ての散乱・吸収の断面積をエネルギーの関数として図4a,b,cで示します。
今回の実験で使うPb, Al, NaIの断面積を示します。
NaIとは次の章に出てくる結晶シンチレーターの断面積です。これで荷電粒子とγ線を代表とする電磁波の相互作用がわかりました。

中性子
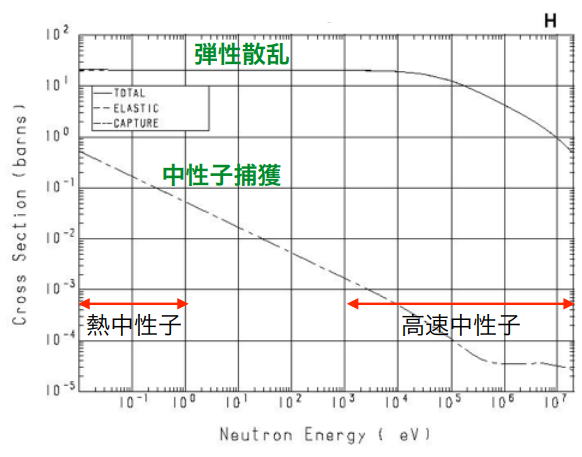
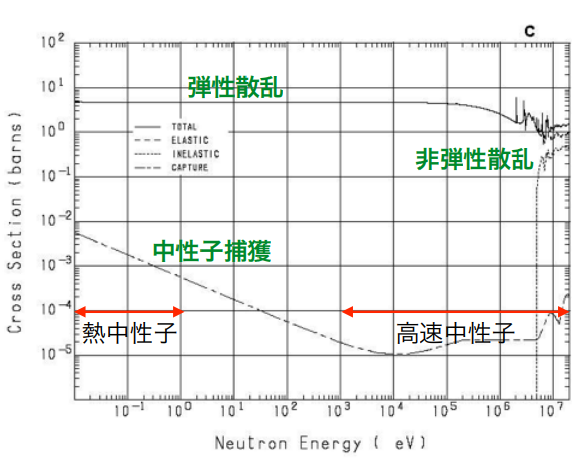
中性子と原子核
の反応確率は、断面積(cross section)と呼ばれている。
さて、中性子と原子核がビリヤードの玉のような剛体球であるとしよう。この場合、中性
子がどのような速さであっても、原子核と衝突する確率は変化しないであろう。仮に、中性
子と原子核の反応確率が(原子核の種類には依存したとしても)中性子の速さによって変化
しなければ、原子炉物理は、はるかに簡単なものになっていたに違いない。
しかしながら、現実には、中性子と原子核の反応確率は、中性子の速さ(エネルギー)に
対して、極めて複雑な挙動を示す場合が多い。原子炉内を飛び交う中性子のエネルギー範囲
は、約 20 MeV~10-5 eV と 12 桁にも及ぶが、単一核種の反応確率であっても中性子のエネ
ルギーによって数桁、値が変化することが一般的である。中性子と原子核の反応には様々な
種類があるが、反応が異なれば反応確率は数桁の大きさで値が変化する。また、中性子のエ
ネルギーが同じであっても、核種により反応断面積はやはり数桁の大きさで値が異なる。こ
のように、中性子と原子核の反応確率は極めて複雑であり、これが原子炉物理を難しいもの
とし、原子炉の設計計算を難しくしている要因の一つでもある。
以下では、まず中性子と原子核の反応確率の考え方を述べ、なぜ反応確率が断面積と呼ば
れているかを説明する。次に、代表的な反応確率(断面積)を例にとって、その特徴を説明
する。
4.2.1 中性子と原子核の反応確率と断面積の関係
お祭りの縁日でよくやっている射的を考えよう(図 4-7)。射的では、コルクの玉を鉄砲で
撃ち、棚に飾ってある景品に当て、景品を棚から落としてゲットする。では、どのような景
品であればゲットし易いであろうか。以下では、話を簡単にするため、景品の重さについて
は考慮せず(全て同じ重さとして)、大きさだけを考えることにする。
容易に想像できるように、景品が大きいほどコルク玉を当て易いであろう。もう少し正確
に言うと、単に大きいというだけではなく、射的をやっている人から見て、景品の面積が大
きいほどコルク玉を当てやすいと考えてよい。ちなみに、大きくても、景品が薄い箱のよう
な形状をしている場合、側面を向けられていれば、玉が当たりにくいため難易度は上がる。
実際に、高い景品の場合は、このようにおいてある場合がある。側面から当てても景品が倒
れないので、二重に難しい。
通常、射的は景品に狙いを定めてそれを落とすわけであるが、仮に目隠しをして射的をす
ることを考えよう。この場合、景品をゲットする確率は格段に下がるものの、やはり射的を
する人から見て、面積が大きい景品に当て易いことは確かであろう。
この「目隠しをして射的をする」状況は、中性子と原子核の相互作用を考える上で直感的
によいモデルになっている。中性子は原子炉の中をランダムに飛行しており(目隠しをして
射的をしている状態であり)、中性子(コルクの玉)が原子核(景品)に衝突するかどうか
を考えるわけである。先の「射的モデル」の議論によると、景品の「面積」が大きいほど当
てやすいということであった。より厳密に言うと、射的をする人から見た景品の「断面積」
が大きいほど当たりやすいということである。
直感的に当たり前のことを言っているように聞こえるかもしれないが、このイメージを
中性子と原子核の相互作用に当てはめることで、両者の反応確率が「断面積」(英語では Cross
section)と呼ばれていることが理解できる。すなわち、原子核の「断面積」が大きいほど反
応確率が高い、ということである。
微視的断面積
前節では、射的モデルを使用して、中性子と原子核の相互作用のイメージを描いた。そこ
で重要であったのは、景品の「断面積」であった。
原子炉物理では、原子核一個の反応確率(景品一個にコルク玉が当たる確率に相当)を微
視的断面積(microscopic cross section)と呼んでいる。詳細は後述するが、まずは、中性子
から見た原子核の「当たりやすさ」と「大きさ」を示しているものと理解しておけばよい。
断面積の単位は、当然ながら、面積であり、SI 単位系では m2 となる。ただし、原子核の
直径は 10-15 m 程度であり、非常に小さい。そのため、原子核の「断面積」は非常に小さい
値になる。このため、原子炉物理では、微視的断面積を表すために barn という単位を用い
る。1 barn は 10-28 m2 もしくは 10-24 cm2 と定義されている。1 barn は、大雑把に言って、ウ
ラン原子核の幾何形状的な断面積に対応している。なお、barn の省略形として、b が用いら
れる場合もある。
微視的断面積は、4.1 節で述べた反応の種類だけある(図 4-8)。核分裂に対しては微視的
核分裂断面積、弾性散乱に対しては微視的弾性散乱断面積、等であり、中性子と原子核の反
応に応じて微視的○○断面積と称される。なお、全ての反応を積算したものは、微視的全断
面積と称される。
【コラム】 barn の語源
「barn」を辞書で調べると、「納屋」と出てくる。納屋と原子核の反応確率がどのように
関係するのであろうか。英語に” couldn’t hit the broad side of a barn”(「大きな」納屋の広い側
面に当てることさえできない)というフレーズがあり、これは、「目的がなっておらず、何
かを達成することが難しい状況」を示すとのことである。
このフレーズに触発され、マンハッタン計画に従事していた科学者が、秘密を保持しつ
つ、(目眩ましもかねて?) ウランの原子核の反応確率(断面積)を表すために、barn を用
いたようである。また、加速器を用いてウランの原子核に粒子を衝突させる実験において
は、ウランの原子核は十分に大きいことも、この barn という単位を採用した理由になって
いたらしい。
巨視的断面積
もう一度射的の話に戻ろう。先ほどは、一個の景品を考え、景品の大きさ(断面積)が景
品に当たる確率に比例することを述べた。さて、射的をやっている店が何軒かあるとしよう。
できるだけたくさん景品をゲットするためには、どのように射的屋を選べばよいであろう
か。話を簡単にするため、全ての射的屋で値段は変わらず、射撃に使用するコルク球の数も
同一であるとする。さらに、全ての射的屋で景品一個の値段と重量は同一で、景品の数はコ
ルク球の数より十分多いとする。ここでの観点は、できるだけ景品の数を稼ぐことである。
なお、普通の射的ではあり得ないが、目隠しをするものとする。
このような条件で考えたとき、選び方としては、①できるだけサイズの大きな(断面積の
大きな)景品が、②できるだけ密集しておいてあり、③景品がおいてある範囲が広く、④景
品までの距離が近いところ、が良さそうに思える。
また、通常の射的には存在しないが、屋根から景品がランダムに吊り下げられている状況
を考える。景品は、床から天井まで、さらに奥行き方向にランダムに吊り下げられているも
のとする。この場合でも、上記と同じく、①景品のサイズが大きく、②密集しており、③景
品がある範囲(体積)が大きく、④景品までが近い、状況が有利である。
これまでの議論で明らかなように、景品一個あたりの断面積が大きいほど、コルク玉は景
品に当たりやすい。景品が密集していれば(理想的には隙間がなければ)、さらに当たりや
すくなるであろう。景品の置いてある範囲が広い(従って、置いてある景品の数が多い)場
合も当たりやすくなるであろう。また、景品までの距離が近いと当たりやすい。
いずれも直感的に当たり前であるが、これを中性子と原子核の相互作用に置き換えて考
える。①は、原子核の微視的断面積が大きいことに相当する。②は、原子核の原子数密度が
大きいことに相当する。③は目標の原子核から構成される物質の体積が大きいことに相当
する。④は、中性子の発生源から物質までの距離が小さいことに対応する。
これらのうち、原子核が構成する物質の性質に対応するものは、①の微視的断面積と②の
原子数密度である。これらが大きいほど、中性子と物質は相互作用しやすくなる。そのため、
原子炉物理では、微視的断面積に原子数密度を乗じた値を巨視的断面積(macroscopic cross
section)として定義している。中性子が物質に入射した場合、巨視的断面積が大きいほど、
物質を構成する原子核と中性子が相互作用しやすくなる。なお、物質に複数の核種が含まれ
ている場合、核種毎にその核種の微視的断面積とその核種の原子数密度を掛け合わせ、これ
を全ての核種について足し合わせたものが巨視的断面積となる。
微視的断面積の単位が「面積(m2
)」であり、原子数密度の単位は「1/体積(1/m3
)」であ
る。従って、これらを乗じた巨視的断面積の単位は「1/長さ(1/m)」となる。長さの逆数を
持つ物理量を「面積」と称しているのはやや違和感があるかもしれない。これは、元々の英
語が macroscopic cross section であり、それを和訳しているためである。巨視的断面積が大き
いほど中性子が原子核と相互作用しやすくなることは、先に述べたとおりである。そこで、
巨視的断面積は、中性子が単位距離進む間に相互作用する確率を示しているものと理解す
ればよい。そうすれば、巨視的断面積の単位が「1/長さ」になっていることが納得できるであろう。
【コラム】 物質中で原子核はまばらにしか存在していない
原子の大きさは大雑把に 10-10 m であり、原子核の大きさは 10-15 m である。つまり、原子
の大きさと原子核の大きさは 105
(10 万倍)の違いがある。
東京ドームのグラウンドの面積は約 13,000 m2 である。東京ドームを原子とすると、原子
核の面積は、概ね 0.1 m2
、つまり、直径 0.35 m の円盤に相当する。グラウンドの中にボー
ルをランダムに投げ入れ、この円盤にボールが当たる確率は極めて低いであろう。すなわ
ち、ある 1 個の原子に中性子が入射しても、原子核と反応を起こす確率は低いと言うことで
ある。
ここまで、中性子と原子核の相互作用を射的のモデルで説明してきたが、実際の原子核
は、射的屋の景品とは比べものにならないほど、まばらにしか存在していないと言うことで
ある。この点を頭に入れておくとよい。
なお、物質を構成する原子核の数は極めて多いため、結果として中性子と物質は「それな
りに」相互作用する。例えば、常温の水の場合、5 cm の厚さがあれば、99.9%程度の中性子
は、水を構成する水素あるいは酸素の原子核と何らかの相互作用をする。
微視的断面積の特徴
ここでは、代表的な微視的断面積について、入射する中性子に対するエネルギー依存性に
ついて説明する。ポイントは以下の 5 点である。
①入射する中性子のエネルギーにより、微視的断面積は大きく変化する。
②微視的断面積(の種類、核種によって微視的断面積は大きく異なる。また、同位体であっ
ても、質量数が 1 異なるだけで微視的断面積は大きく異なる。
③原子核に入射する中性子のエネルギーが低いほど微視的断面積が大きくなる場合が多い。
すなわち、エネルギーの低い中性子の方が、原子核と反応しやすい場合が多い。
④質量数が大きくなるほど、微視的断面積のエネルギー依存性は複雑となる。また、特定の
中性子エネルギーに対して、反応確率が非常に大きくなる場合がある。
⑤中性子の入射エネルギーが大きい場合にのみ、微視的断面積がゼロでない値を持つ場合
がある。
以下では、微視的断面積の種類ごとに大まかなエネルギー依存性と、そのような振る舞い
を示す理由を述べる。また、代表的な核種について、微視的断面積を図 4-10~4-15 に図示
する。微視的断面積は、中性子のエネルギー範囲が広いこと、また微視的断面積の値が中性
子の入射エネルギーに対して大きく変化することから、横軸(入射中性子のエネルギー:
eV)、縦軸(微視的断面積:barn)ともに対数で表示するのが一般的である。
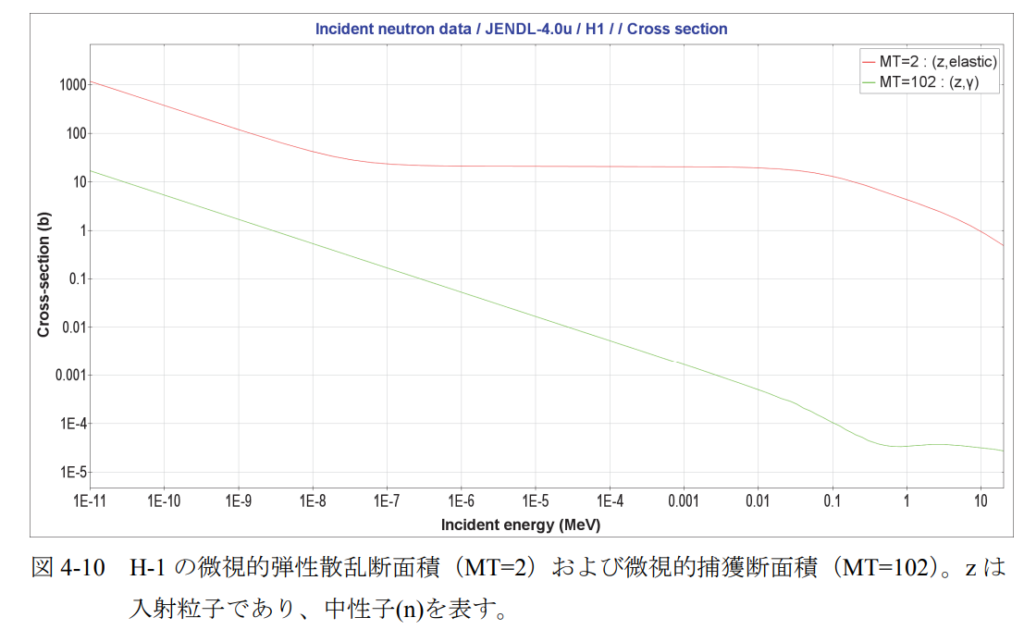
(1)微視的弾性散乱断面積
おおよそ、0.1 MeV~10-8 MeV(10-6 eV)程度のエネルギー範囲で一定値を取る(例:図
4-10)。0.01 eV~0.001 eV 以下では、中性子のエネルギーが小さくなるほど微視的断面積は
大きくなる。核種ごとの差異は、後述の捕獲断面積などに比べて小さい。
(2)微視的捕獲断面積
基本的に中性子のエネルギーが小さくなるほど、微視的捕獲断面積は大きくなる。多くの
場合、微視的断面積は、入射する中性子の速さの逆数に比例する。このような微視的断面積
のエネルギー依存性を「1/࢜依存性(1/࢜ law)」と呼んでいる(例:図 4-10)。質量数が大き
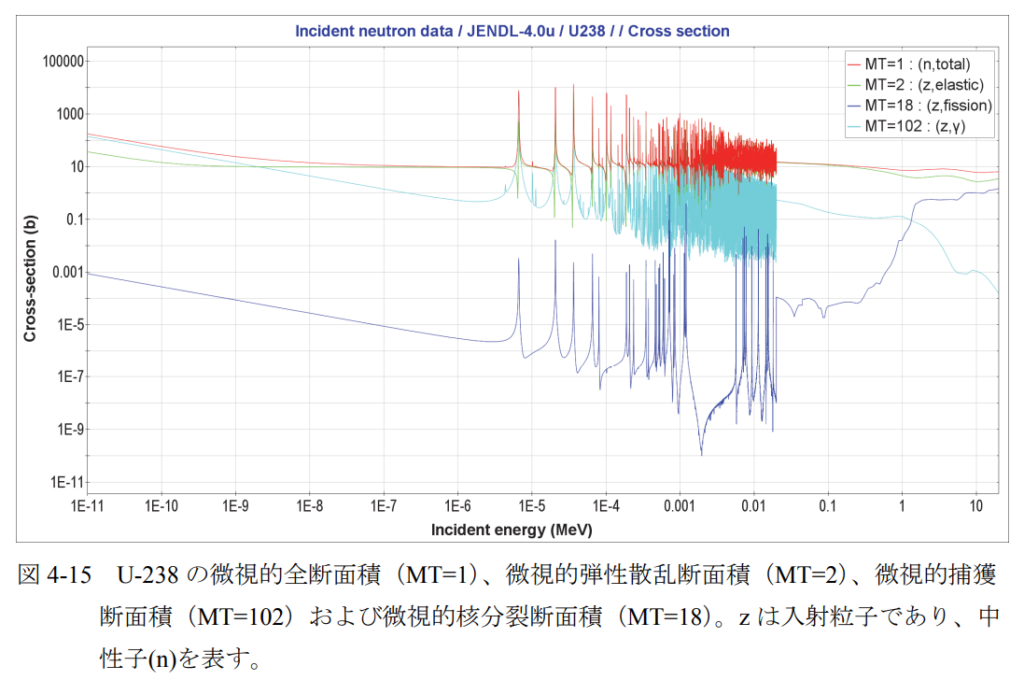
な核種については、1 eV~1,000 eV 近辺で非常に複雑な挙動を示す(例:図 4-15)。特定の
中性子エネルギーに対して、微視的断面積が極端に大きくなる現象は、共鳴(resonance)と
呼ばれており、微視的断面積に共鳴が見られるエネルギー領域を共鳴領域と呼んでいる。な
お。1/ݒ依存性は、共鳴領域より低いエネルギー領域で見られる。
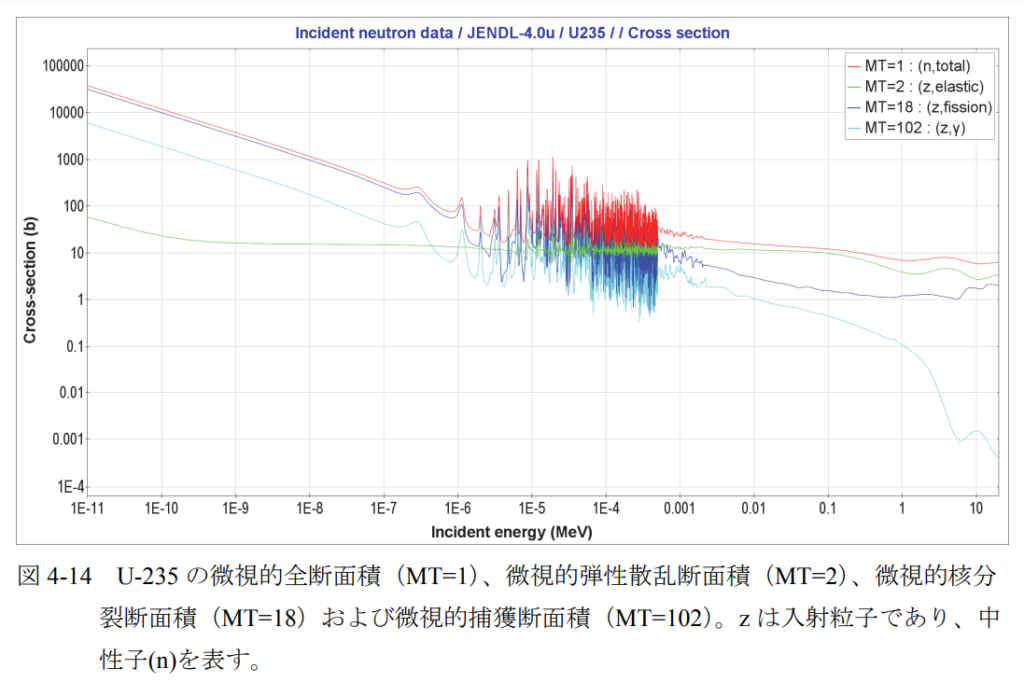
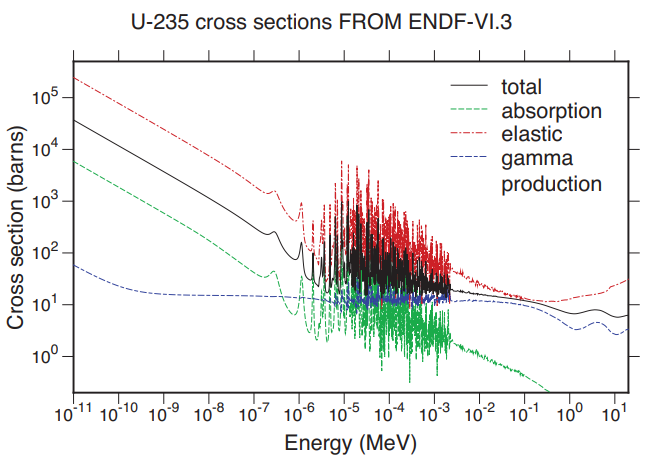
(3)微視的核分裂断面積
核分裂を起こす核種のうち、U-235 など質量数が奇数の核種については、微視的捕獲断面
積と類似の挙動を示す(例:図 4-14)。すなわち、エネルギーの低い中性子に対して、微視
的核分裂断面積は大きくなる。また、微視的核分裂断面積は、入射する中性子の速さの逆数
に概ね比例する。一方、核分裂を起こす核種のうち、U-238 等、中性子数が偶数の核種につ
いては、低エネルギーの中性子に対して微視的核分裂断面積はほぼゼロであり、一方、高エ
ネルギーの中性子に対して微視的核分裂断面積が大きくなる(例:図 4-15)。すなわち、高
エネルギーの中性子に対しては核分裂が生じるが、エネルギーの低い中性子では核分裂が
発生しないことになる。なお、高エネルギーの中性子のみで発生する反応をしきい反応
(threshold reaction)と呼ぶ。
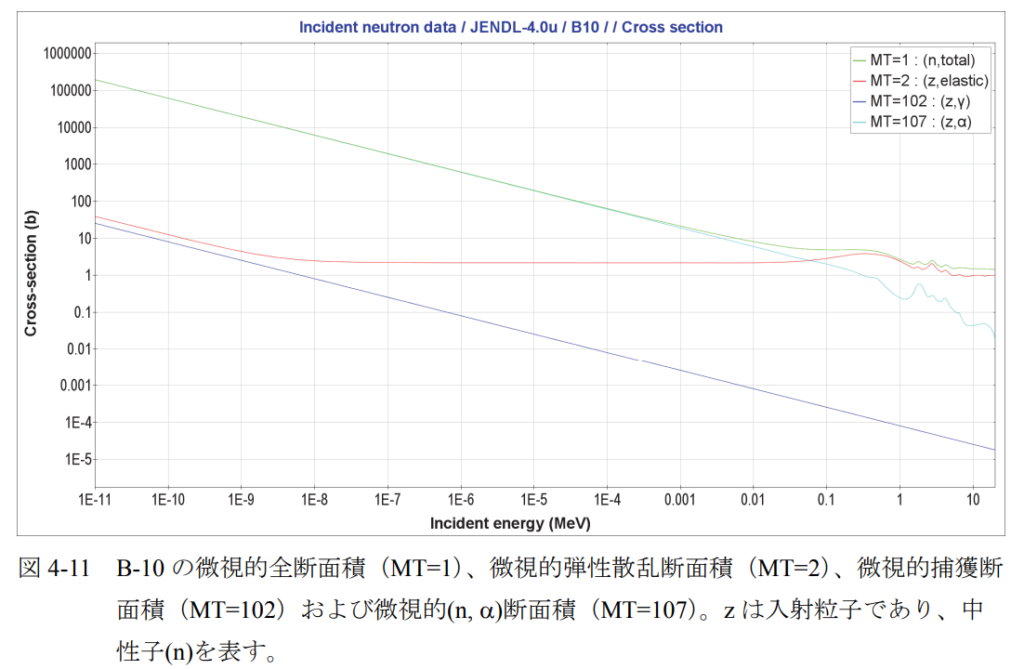
(4) (n, )反応断面積
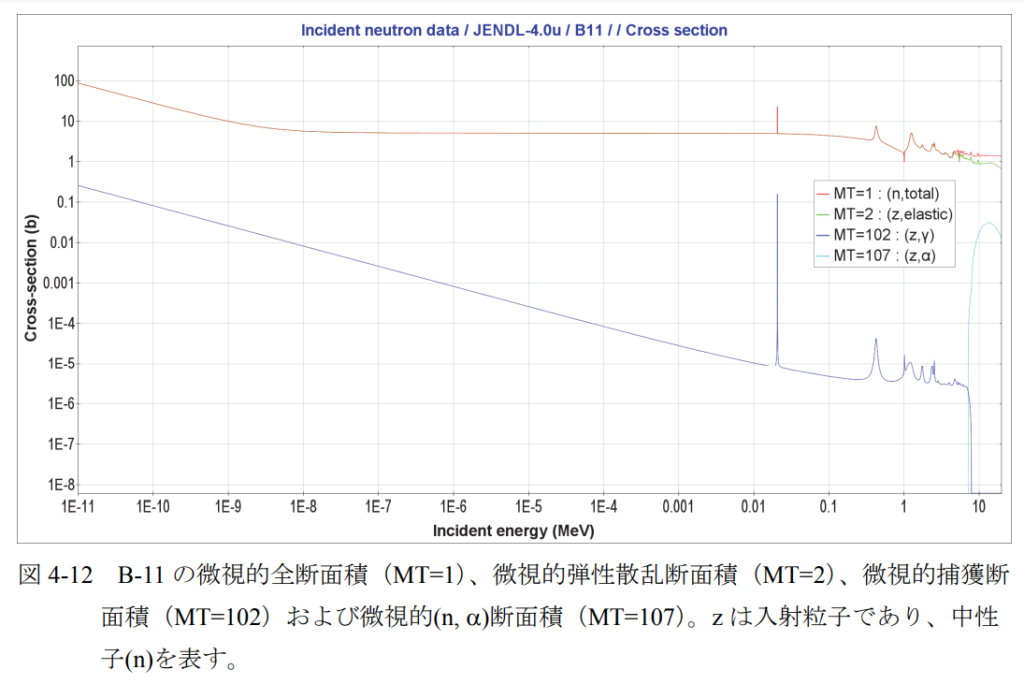
B-10 など、特定の核種については、反応のほとんどを(n,)反応が占めている(例:図 4-
11)。ただし、質量数が 1 変わるだけで(n,)反応の大きさは大きく変化する(例:図 4-11, 4-
12)。1/ݒ依存性を示す場合がある。
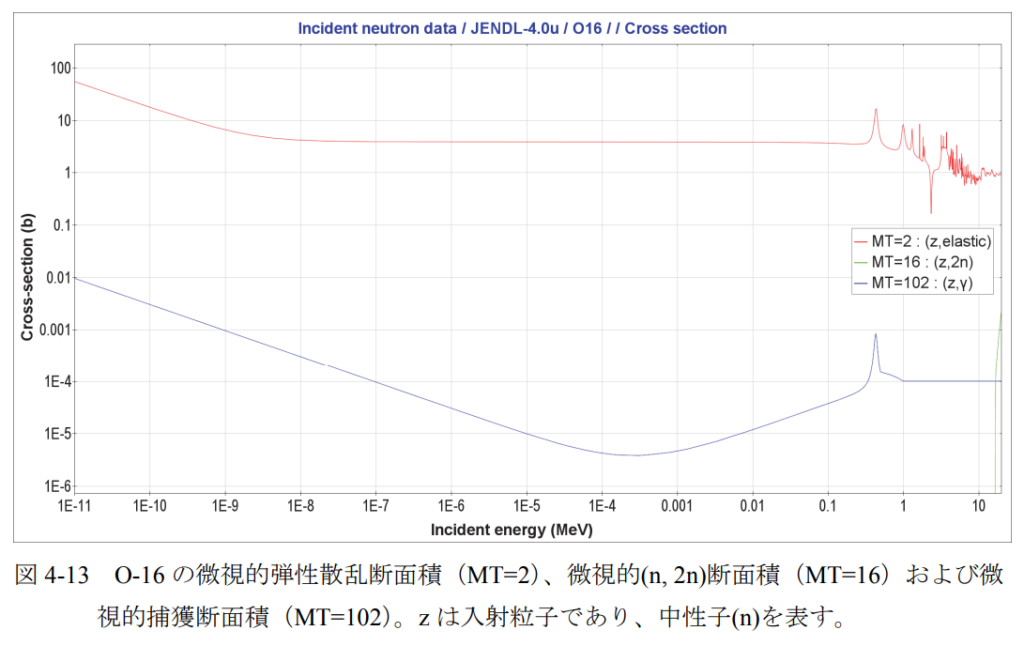
(5) (n,2n)、(n,3n)反応断面積
入射する中性子のエネルギーが高いときに限って発生するしきい反応である。図 4-13 の
O-16 に対する(n,2n)反応の断面積で、このような特性を見ることが出来る。


コメント