放射線(電離放射線)は物質と様々な反応(相互作用:Interaction)を起こしエネルギーが減衰していきます。
相互作用の仕組みは入射する放射線の種類(荷電粒子、光子、中性子の3種類)で分けられます。
荷電粒子の相互作用
荷電粒子とは、電荷を帯びた粒子です。代表的な荷電粒子は電子やベータ粒子、アルファ粒子(ヘリウム原子核)です。
電離・励起(衝突損失)
荷電粒子が標的の原子を通過する時に、原子中にある電子にエネルギーを与えて弾き出す働きを電離作用(イオン化)と呼び、残った原子はプラスの電荷をもった原子(イオン)になります。
また、電子が外側の軌道に遷移し、原子全体のエネルギーが高くなることを励起作用と呼びます。
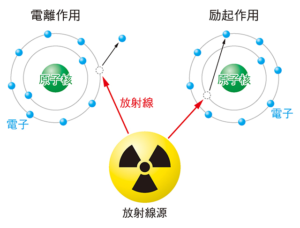
このように、荷電粒子の相互作用によって物質中の原子が電離や励起を起こすことを「エネルギーが与えられる」といいます。
W値
荷電粒子が気体の中を通過すると、飛跡に沿って気体が電離されます。このとき荷電粒子はエネルギーを消費し、気体はエネルギーを与えられています。
荷電粒子がどのくらいエネルギーを消費するのかは、荷電粒子と気体の組み合わせによって異なります。
W値は、特定の気体が特定の荷電粒子から与えられるエネルギーの大きさを表します。
例えば、電子線が空気中の原子を一つ電離させるとき、エネルギーを34eV消費します。アルファ線の場合は36eV消費します。
W値が大きいほど荷電粒子が気体に与えるエネルギーが大きいことを表します。
W値は元素によって大きく変化せず、また入射エネルギーの大きさにもよらず、ほとんど一定で約30eVと覚えます。
W値は荷電粒子が1つのイオン・電子対を生成する(電離する)ために消費するエネルギーで、次の式で表されます。
W=EN
E:荷電粒子が失ったエネルギー
N:生成したイオン・電子対の数
イオン化エネルギー
W値はイオン化エネルギーに対応します。
原子や分子を電離させるために必要なエネルギーはイオン化エネルギー(電離エネルギー・イオン化ポテンシャル・電離ポテンシャル)と呼ばれます。
イオン化エネルギーが高いほど、原子や分子が保持する電子が強く束縛されているため、イオン化しにくいことを意味します。
気体が電離しやすい(イオン化エネルギーが小さい)ほど、電離のために消費するエネルギーが少なくて済むため、W値が小さくなります。
希ガスは安定元素で電離しにくい(イオン化エネルギーが大きい)ので、同じイオン周期の中で最もW値が高くなります。
また、希ガスの中では原子番号が大きいほど不安定になり電離しやすくなる(イオン化エネルギーが小さい)ため、W値が低くなります。
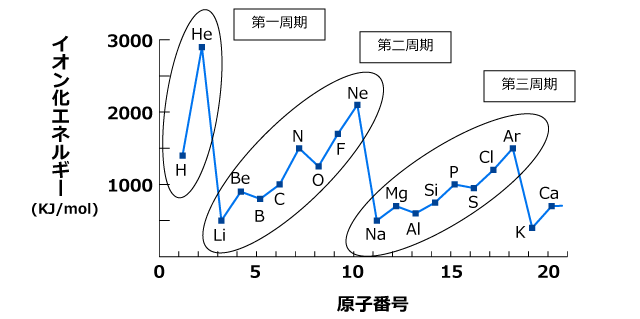
イオン化エネルギー(電離に必要なエネルギー)がW値(電離のために失うエネルギー)の半分程度なので、放射線の半分ほどのエネルギーが電離以外の相互作用で消費されていることが分かります。
ε値
W値は気体に対する値であるのに対し、荷電粒子が固体中に1つのイオン対をつくるときに費やされる平均エネルギーをε値といいます。
W値と同様に、ε値も次の式で表されます。
ε=EN
参考:種々の気体におけるイオン化エネルギーと、電子・α粒子・陽子のW値
種々の気体における電子・α粒子・陽子のW値

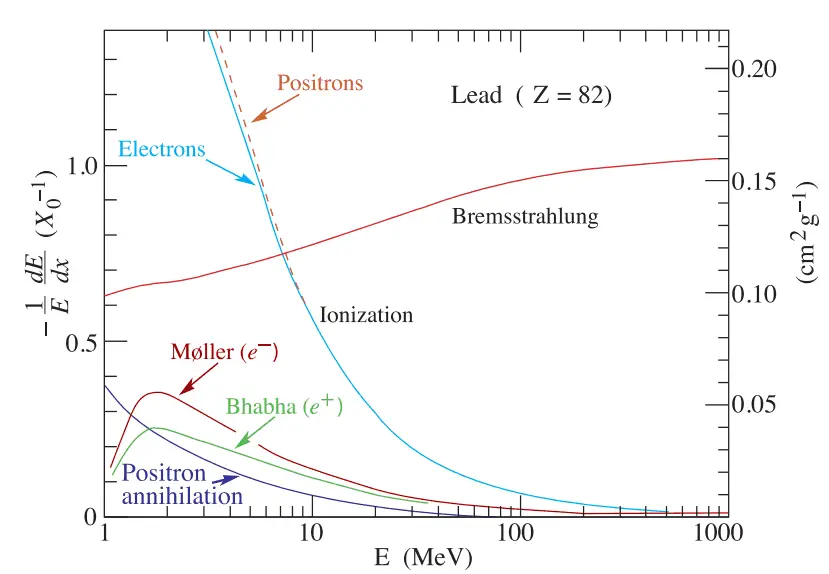
制動放射(放射損失)
荷電粒子が物質内の原子核や電子が作る電場の影響を受けて曲げられ、減速する際に余分なエネルギー(X線)を放出します。これを制動放射(制動輻射/Bremsstrahlung)と言います。
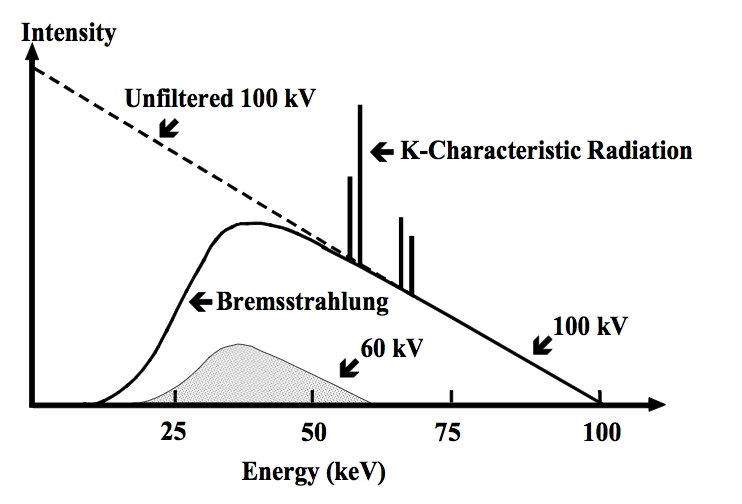
連続スペクトルです。
電子対消滅
陽電子(positron) は電子(electron) の反物質で、質量・スピンは電子と等しく、正の電荷を持っています。
陽電子が物質に入射すると電子と結合し、2本以上の光子(消滅放射線)を出して消滅します。
消滅放射線の数が2本の場合、放出される光子は正反対の方向に放出され、どちらもエネルギーは511keVです。
荷電粒子反応(核反応)
α線のように比較的エネルギーの小さな荷電粒子でも、ターゲットとなる原子核の原子番号が小さい場合はターゲット核周辺の電場が小さいため、相手の原子核と接触し、核反応を生ずることがある。
9Be
中性子を放出しやすい特異な原子核で、α線と9Be(α,n)12C反応を起こす。この核反応は中性子生成反応であり、α線放出核種である241Amと9Beの混合物を密封したものは中性子源としてよく使われる。
65Znの生成
放射性核種である65Znは、銅ターゲットに陽子(p)や重陽子(d)ビームを照射し、65Cu(p,n)65Znあるいは65Cu(d,2n)65Zn反応を利用して生産される。
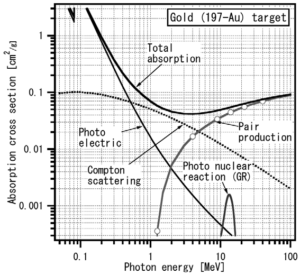
光子の相互作用
光子(ガンマ線・X線)は波の形で存在する、質量や電荷を持たないエネルギーの粒です。
波のような性質と粒子のような性質(粒子と波動の二重性)を併せ持つため、物質との相互作用が複雑です。そのため光子が持つエネルギーが大きくなるにつれ、主な相互作用の特徴が波動性から粒子性へと変化していきます。
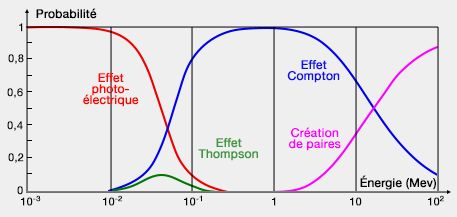
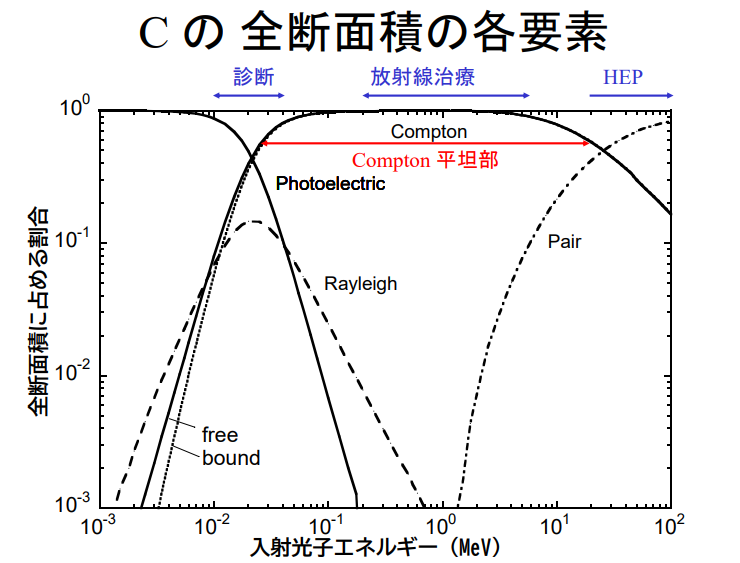
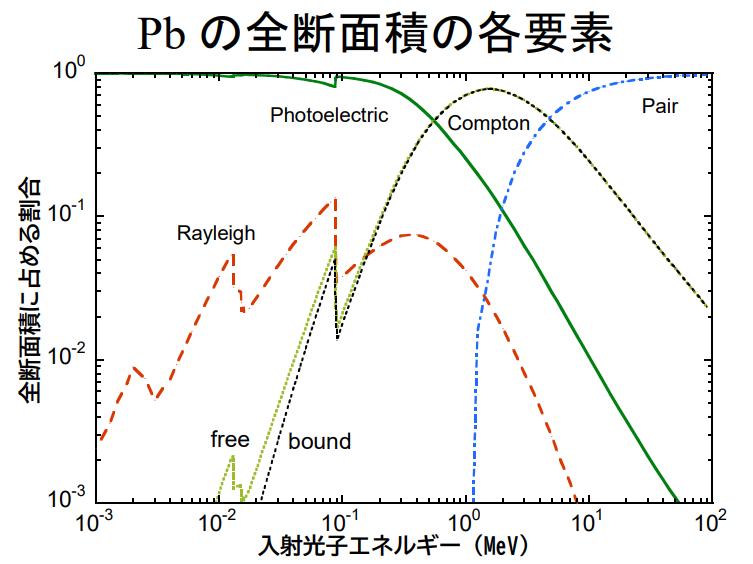
低エネルギー領域ではレイリー散乱、光電効果が主であり、次第にコンプトン散乱が主な相互作用となり、高エネルギーでは電子対生成が主となります。
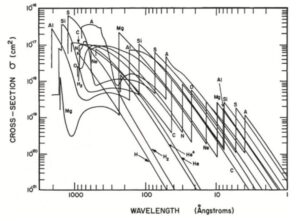
光子と物質との相互作用は次の図で表されます。
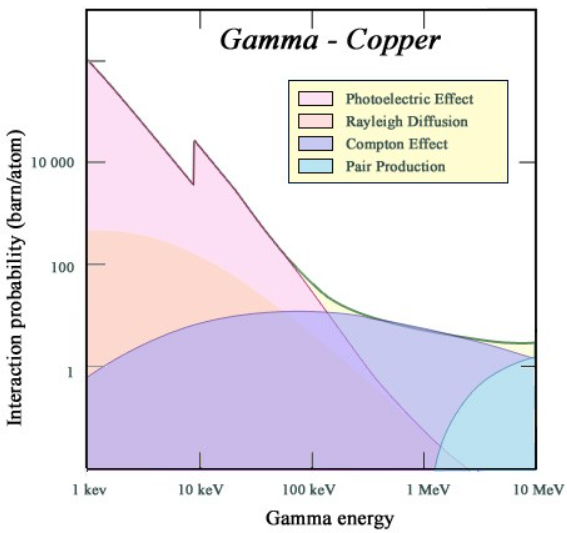
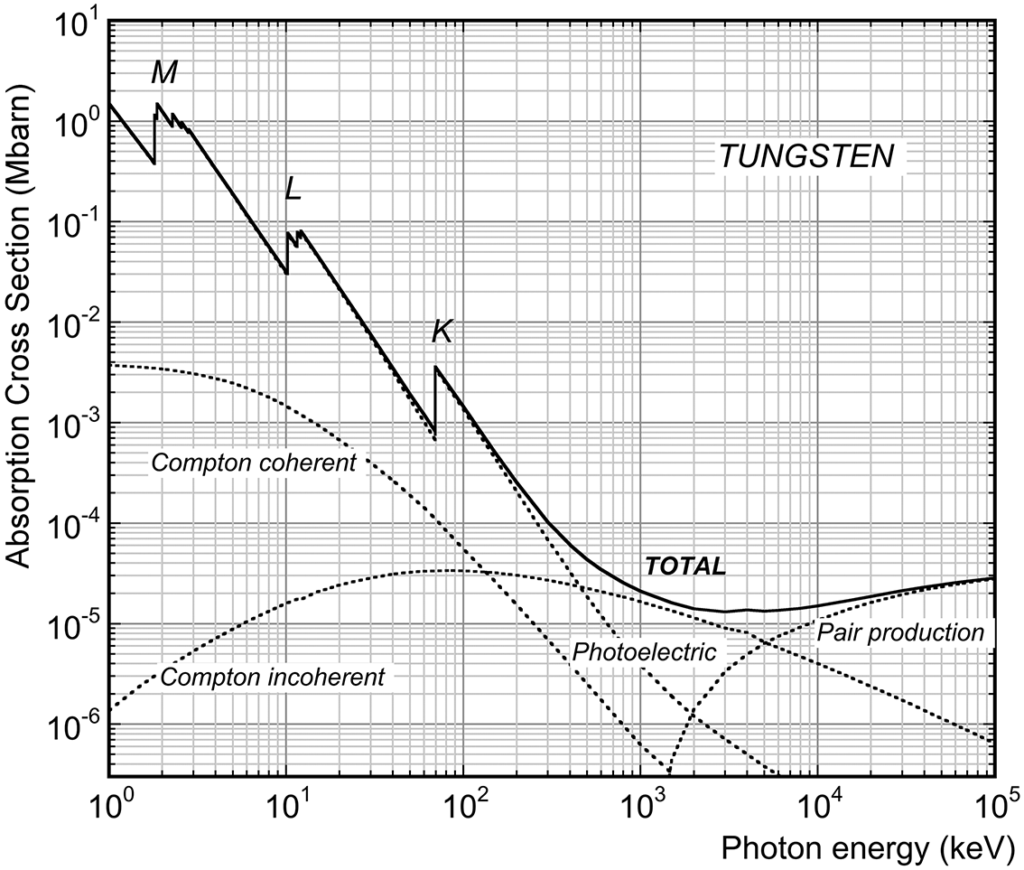
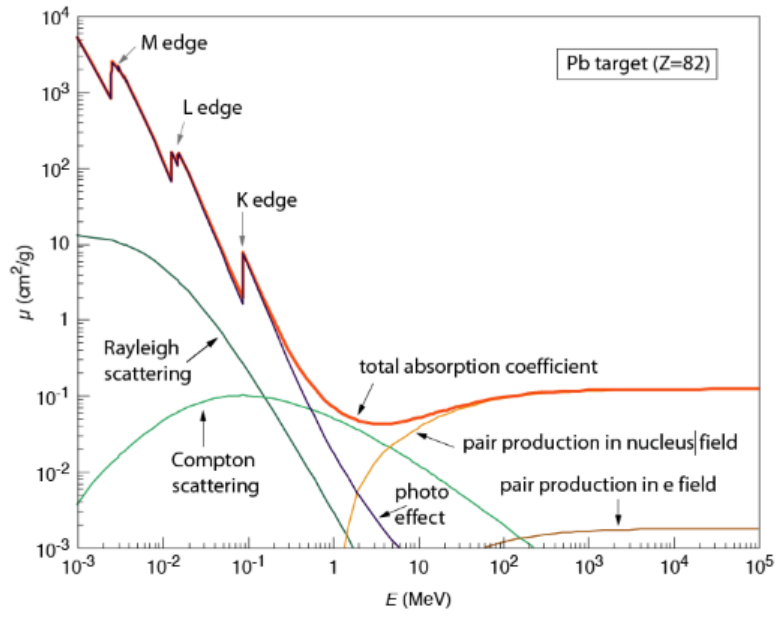

入射光子エネルギーと質量減衰係数(質量減弱係数)の関係
mass attenuation coefficient vs photon energy
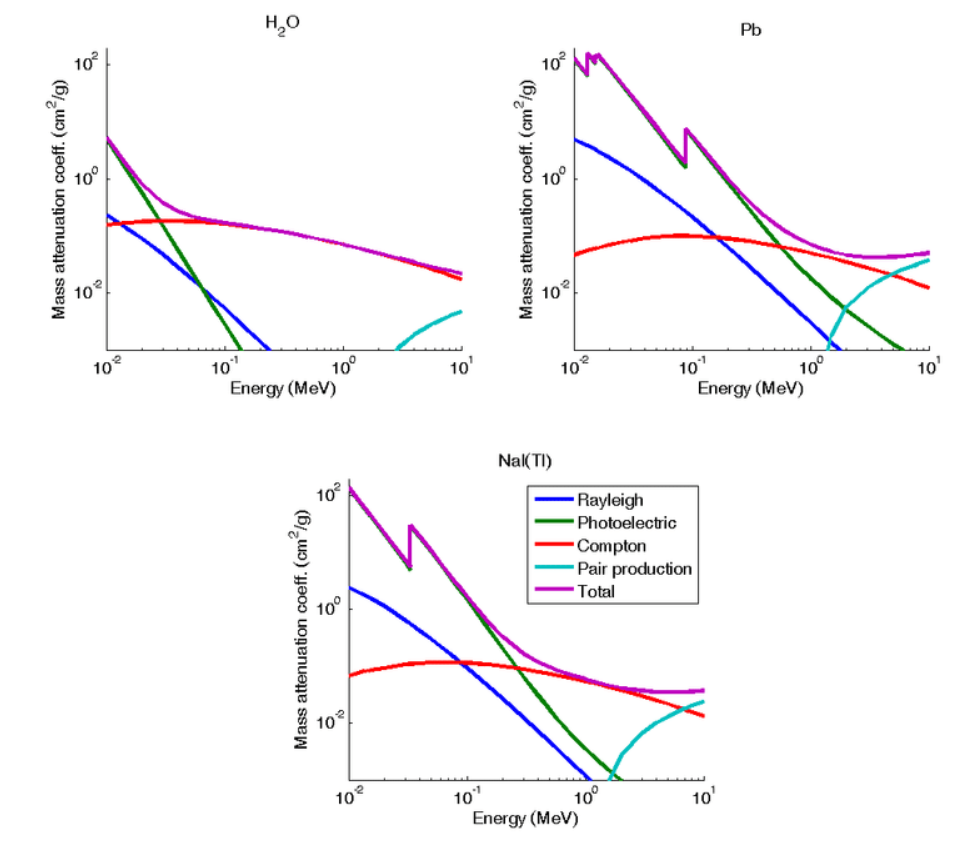

※質量減弱係数は、物質中で入射光子の束密度が減衰する割合(線減弱係数)を物質の密度で割ったもので、物質の違いを無視することができます。
干渉性散乱(レイリー散乱・トムソン散乱)
Coherent Scattering
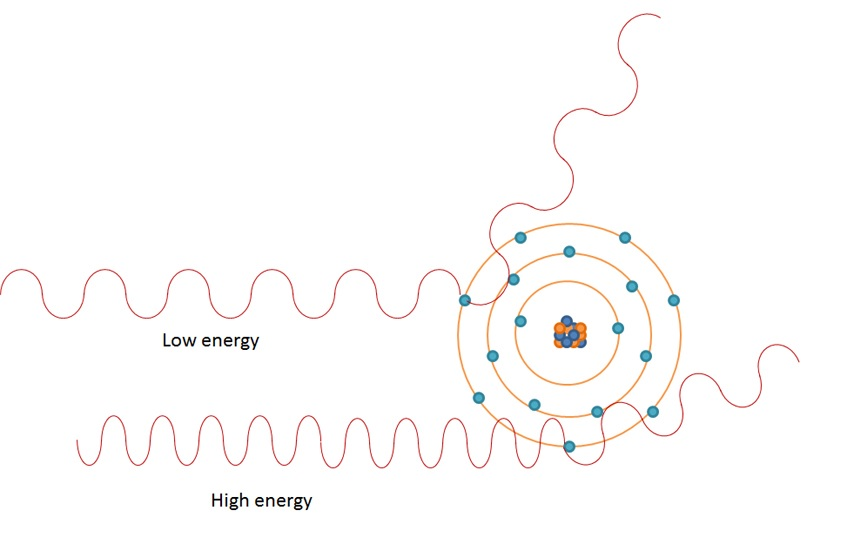
低いエネルギー領域では、光子が標的に衝突した後、光子のエネルギー(波長)は変化せずに方向だけが変わります。これを弾性散乱といいます。
干渉性散乱は光子の波動性による相互作用で、電子が光を反射する現象です。
軌道電子との弾性散乱はレイリー散乱と呼ばれます。また、束縛を受けていない自由な荷電粒子との弾性散乱はトムソン散乱と呼ばれます。
入射光子のエネルギーが高くなると散乱光子の波長が短くなり、コンプトン散乱(非干渉性散乱)へと変化します。
非干渉性散乱(光電効果・コンプトン散乱)
光電効果

Photoelectric Effect
入射してきた光子(X線やガンマ線)が原子に吸収され消滅し、軌道電子が軌道から飛び出る現象です。この電子は「光電子」と呼ばれます。
光電効果は原子と衝突する現象で、光が粒子としてふるまう性質を持っていることが分かります。
光電効果は入射光子のエネルギー(振動数が大きいほどエネルギーが大きい)が軌道電子の束縛エネルギーより大きくないと起きません(下図の赤波)。
また、このとき飛び出た光電子の運動エネルギーは、光子のエネルギーから軌道電子の束縛エネルギーを消費した残りのエネルギーです。
光電効果は非弾性散乱で、反応前後でエネルギーと運動量を保存するためには原子核がそれを担う必要があります。
つまり標的の軌道電子が原子核に束縛されている必要があります。例えば自由電子単独を標的とする場合、光子は消滅せずに散乱を起こします。
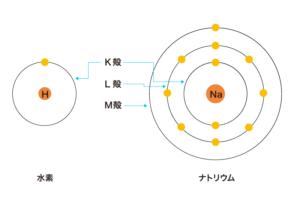
軌道電子と原子核の束縛が強いほど原子核が保存に関与できます。そのため複数の殻で光電効果が可能なときは、束縛エネルギーが大きい内側の殻ほど起こりやすくなります。
入射光子のエネルギーが大きくなるにつれ相対的に束縛エネルギーが小さくなるため光電効果が起きづらくなり、コンプトン散乱が起こってきます。

波長と領域
軌道電子の束縛エネルギーは一定の値であるため、光電子のエネルギーは一定(線スペクトル)になります(光電ピーク)。
例えばエネルギーが100keVの光子を鉛に入射した場合、K殻(束縛エネルギーは88keV)から飛び出る光電子のエネルギーは12keVで一定となります。
特性X線とオージェ電子
軌道電子が飛び出た後の空孔は、外殻から軌道電子が遷移して、余った束縛エネルギーの差が特性X線やオージェ電子として放出されます。
この現象は、必ずどちらかが起こる競合過程です。
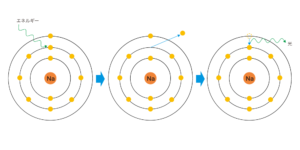
また、原子番号が小さい核種ほど、核が電子を引きつける力が弱いため、原子番号が小さい核種ほど
オージェ電子の放出率が高くなります。
特性X線とオージェ電子のうち、特性X線を放出する割合を、蛍光収率といいます。
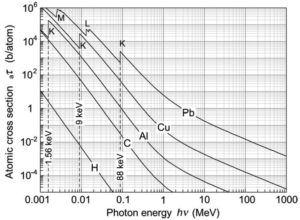
光電効果の原子断面積τ

また、入射光子エネルギーの-3.5乗に比例します。
断面積(反応の起こりやすさ)は物質の原子番号Zの5乗に比例します。


コンプトン散乱
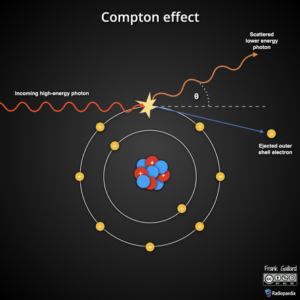
コンプトン散乱(コンプトン効果)は、入射光子が電子にエネルギーを『一部』与えて弾き出し、光子自身も散乱される現象です。
このとき弾かれた電子はコンプトン電子(反跳電子)と呼ばれ、散乱した光子は「散乱光子」と呼ばれます。
散乱光子は最初よりエネルギーが小さくなる(波長が長くなる)ので非弾性散乱(非干渉性散乱)です。
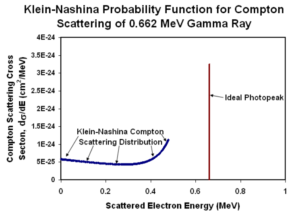
コンプトン電子のエネルギーは、入射した光子線のエネルギーから散乱光子のエネルギーを引いたものになります。この電子のエネルギーは連続スペクトルとなります。
散乱光子のエネルギーは次の式で表されます。
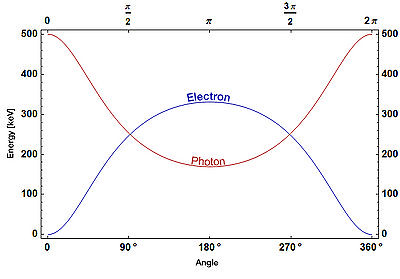
E′γ=Eγ1+Eγ(1−cosθ)m0c2≒Eγ1+2Eγ(1−cosθ)[MeV]
反跳電子のエネルギーは次の式で表されます。
Em=Eγ1+m0c2Eγ(1−cosθ)
コンプトンの式導出
反跳電子のエネルギーは180°で最もエネルギーが高くなります。
コンプトン散乱の断面積σ
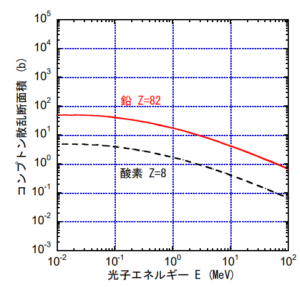
物質中のコンプトン散乱の散乱角に対する散乱確率は標的中の電子数に依存するので、原子1個当たりに対する散乱断面積は標的を構成する原子番号Zに比例します。
X線のコンプトン散乱による微分断面積は次式のクライン・仁科の式で与えられる。
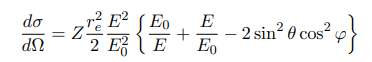
φは入射X線の偏光方向と散乱X線の進行方向のなす角です。φ = 90◦, 270◦のときに散乱確率が最も大きくなり、φ = 0◦、180◦ のときに最も小さくなります。つまり、コンプトン散乱を起こしたX線は偏光方向に対して垂直に散乱される確率が高くなります。
電子対生成

Pair Production
入射してきた光子が原子核の強い電場に吸収されて、「電子」と「陽電子」が生成され飛び出す現象です。
電子対生成の条件は、入射光子は1.02 MeV(陽電子と電子の静止質量の和=2mc2に相当)以上のエネルギーが必要で、これを超えた分のエネルギーは電子対の運動エネルギーに分配されます。運動エネルギーは一定の値を持たないため連続スペクトルとなります。
これにより生成された陽電子は、後に電子対消滅を起こします(荷電粒子で前述)。
電子対生成の断面積κ
断面積(反応の起こりやすさ)は物質の原子番号Zの2乗に比例します。

三対子生成

三対子生成は2.044 MeV(陽電子と電子の静止質量の和の2倍=4mc2に相当)以上のエネルギーをもつ光子が物質に入射したとき、軌道電子を反跳させると同時に電子対生成を起こす現象です。
光核反応(核反応)
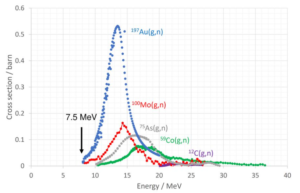
Photonuclear Reaction
光子エネルギーが20MeV付近で核全体の振動励起にあたる状態があるため、この値の付近で共鳴吸収が起こり、光核反応の起こる確率(反応断面積)が最大となります。

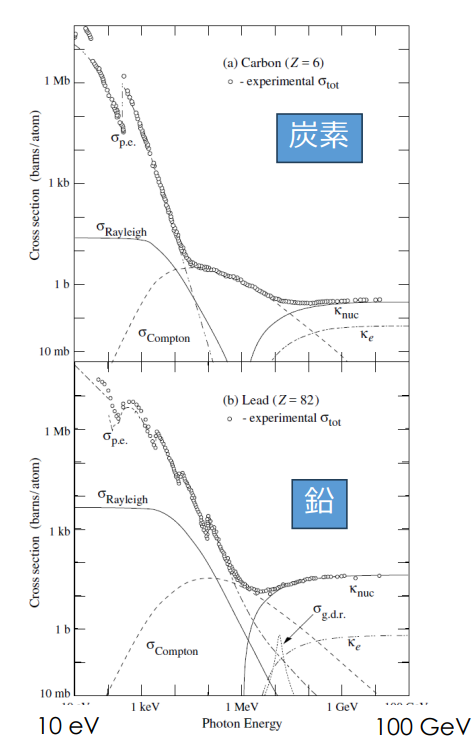
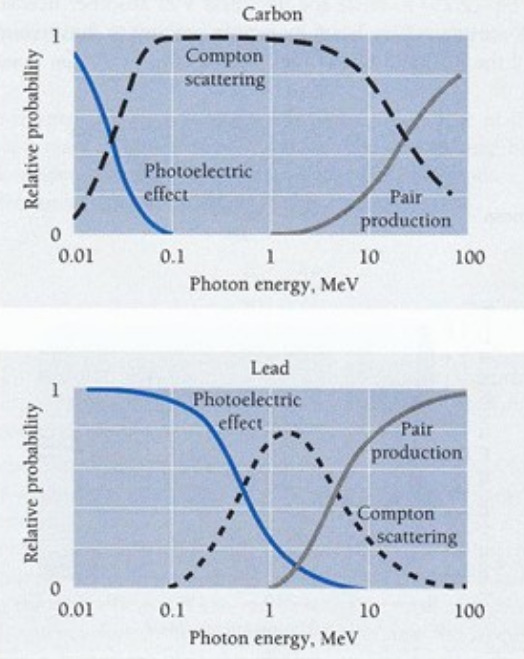
軽い物質と光子の相互作用
30 keV以下は光電効果
0.1 – 10 MeVはコンプトン反応が主要な反応
30 MeV以上は電子対生成
重い物質と光子の相互作用
1 MeV以下は光電効果
1 MeV付近の狭い範囲がコンプトン反応
数 MeVを超えると電子対生成
10 MeV付近に原子核反応からの寄与 (巨大双極子共鳴)
中性子の相互作用
https://rpg.jaea.go.jp/else/rpd/others/study/text_data/text_each/chap4_20191224.pdf

中性子と物質の相互作用は「核反応」です。
核反応は中性子の持つエネルギーの大きさによって反応の種類が変わります。


Chuseishi_5
詳しくは上記の中性子の記事を参照してください。
核反応を考えるとき、
「核反応式」と、「エネルギー(Q値)」を理解する必要があります。
Q値
原子核A(標的核)に粒子aが衝突して、原子核B(生成核)が生成され、粒子bが放出されるときの核反応 A(a,b)B の前後で質量に差が生じたときに、この差に相当するエネルギーをQ値といいます。
MAc2+Mac2=MBc2+Mbc2+Q
Q>0の時を発熱反応、Q<0の時を吸熱反応といいます。
弾性散乱反応(n, n)
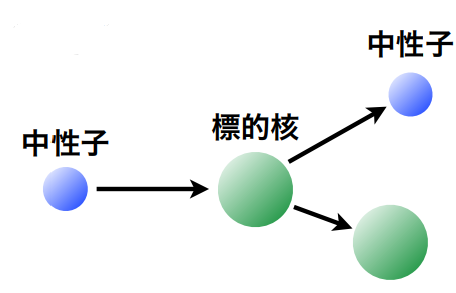
aとbが同じ粒子でQ=0の場合は弾性散乱です。
弾性衝突は、衝突前後で運動エネルギーと運動量が保存されます。
中性子による弾性散乱において、原子核が受ける反跳エネルギーを問われることが多いです。
エネルギー「En」、質量「m」の中性子が、質量「M」の原子核と弾性散乱衝突して衝突前の原子核の進行方向に対して「θ」の方向に散乱した場合に、原子核が受ける反跳エネルギー「E」は次の式で求めることができます。
各粒子・原子核の結合エネルギーをB(Ma)、B(MA)、B(Mb)、B(MB)とします。
主な原子核の結合エネルギーを表にまとめました。
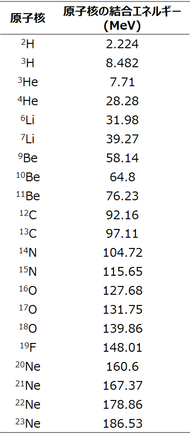
Chuseishi_busshitsu_1
この表での原子核の結合エネルギーは、
次のグラフの「核子1個あたりの結合エネルギー」x「質量数」で計算しています。
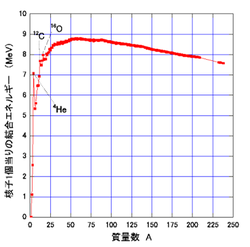
(グラフの出典:L.Glasstone, A. Sesonske “Nuclear Reactor Engineering”)
非弾性散乱反応(n, n’)

非弾性衝突は、衝突前後で運動量のみ保存されます。
中性子捕獲反応(n,γ)
中性子が原子核に取り込まれてγ線を放出する核反応です。
中性子捕獲反応は、一般的にQ値が正の発熱反応です。
中性子放射化反応
原子核による中性子捕獲核反応を応用した元素分析法
放射能を持たない同位体が放射線を受けて放射性同位体になる核反応です。
(中性子を受けて放射化する場合は中性子捕獲反応のひとつです)
放射化反応は、Q値が負の吸熱反応です。
原子核の数N、放射化断面積σ[cm2]の物質に、
束密度がf[1/cm2/s]の中性子を照射したときに、
放射化した物質が持つ放射能A[Bq]は、
中性子の照射時間をt[s]、生成した各種の半減期をT[s]とすると、次の式で表すことができます。
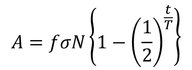
核分裂反応(n, x)

衝突前後で運動エネルギーが保存されます。
ウランやプルトニウムのように重い原子核で生じます。
核分裂の直後に、原子核から2~3個の速中性子が放出されます。
この中性子を「即発中性子」と言い、平均エネルギーは1.98MeVです。
核分裂反応の例を2つ挙げておきます。



コメント