質量数A
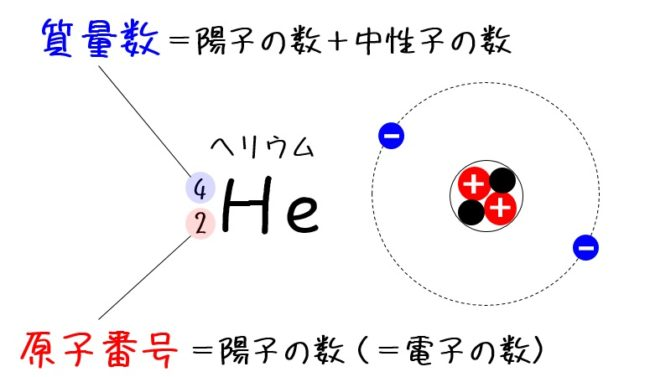
原子核を構成する核子(陽子と中性子)の個数。
統一原子質量単位 [u]
安定した炭素原子核12C(質量数12)の質量を12[u]とし、核子一個の平均質量にあたる1[u]を統一原子質量単位としました。
相対原子質量
他の同位体や原子核の質量を統一原子質量単位[u]で表したものを相対原子質量と言います。
例えば12C(陽子6個,中性子6個)の同位体である13C(陽子6個,中性子7個)は13.003[u]となります。
また、13N(陽子7個,中性子6個)は13.003[u]となり、13Cとの差はほぼありません。
陽子と中性子はほぼ同じ質量なので、質量数Aが1つ増えると相対原子質量はおよそ1[u]増えると考えられます。

12Cから中性子1個が増えた13Cの質量がぴったり13.000[u]とならず13.003[u]となるのは、中性子の質量が1.087[u]で、陽子の1.007[u]よりわずかに重いためです。
また、中性子が1個増えると合計13.087[u]となるはずですが、原子核は核子が増えることによる質量欠損によって、若干質量が減少します。
原子量
炭素原子の安定同位体には12C(相対原子質量=12.0[u])の他にも13C(相対原子質量=13.0[u])などが存在します。
実験をするときにこれらの同位体を分離することが難しいため、安定同位体の天然存在比を考慮した相対原子質量の平均値を原子量として定義しました。
炭素の原子量
炭素原子の安定同位体には12C(相対質量=12.0[u])と13C(相対質量=13.0[u])があり、それぞれの天然存在比が99%、1%だとします。
これは炭素原子が100個あれば、12Cが99個、13Cが1個あるということです。
そして相対原子質量12.01[u]の炭素原子が100個あると考えて計算することができます。
塩素の原子量
塩素原子の安定同位体には35Cl(相対原子質量=35.0[u])と37Cl(相対原子質量=37.0[u])があり、それぞれの天然存在比が75%、25%だとします。
これは塩素原子が100個あれば、35Clが75個、37Clが25個あるということです。
そして相対原子質量35.5[u]の塩素原子が100個あると考えて計算することができます。
ベリリウムの原子量
ベリリウムの安定同位体には9Be(相対原子質量=9.0[u])の一つしかなく、天然存在比は100%です。
これは相対原子質量9.0[u]の塩素原子が100個あると考えて計算することができます。
安定同位体が一つしかない原子は相対原子質量がそのまま原子量となります。
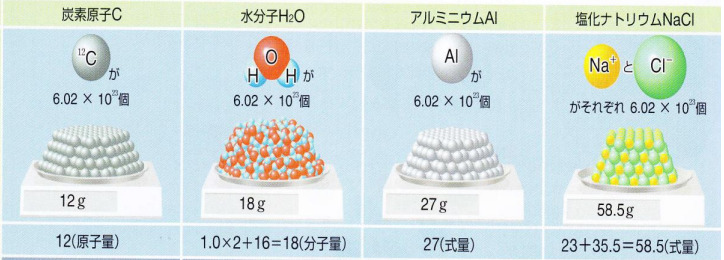
アボガドロ数\(N_A\) [個/mol]
12C(質量数12の炭素)原子核を12[g]集めると、その中に含まれる炭素原子核の数は6.0×1023[個]あります。
これをアボガドロ数と言い、またこの数を1[mol]という単位とします。
モル質量 [g/mol]
アボガドロ数の定義のように、一種類の原子を1mol集めると、その原子の相対原子質量と同じ数値の質量[g]になります。
この物質1mol分の質量のことをモル質量[g/mol]といいます。
モル質量=相対原子質量≒質量数
一つの同位体に着目する場合は、モル質量は相対原子質量と同じで、ほぼ質量数Aと同じです。
12C(質量数12,相対原子質量12[u])原子核を1mol(6.02×1023[個])集めると、質量は12[g](モル質量)。
モル質量=原子量
複数の安定同位体を含む天然組成の原子の場合は、モル質量は原子量と同じです。
天然組成の12Cと13C(原子量12.01[u])原子核を1mol(6.02×1023[個])集めると、質量は12.01[g](モル質量)。
12C(質量数12,相対原子質量12.000[u])のモル質量は12.000[g] ←定義
13C(質量数13,相対原子質量13.000[u])のモル質量は13.003[g]≒13[g]
天然組成の12Cと13C(原子量12.01[u])のモル質量は12.01[g]
35Cl(質量数35,相対原子質量34.97[u])のモル質量は34.97[g]≒35[g]
37Cl(質量数37,相対原子質量36.97[u])のモル質量は36.97[g]≒37[g]
天然組成の35Clと37Cl(原子量35.5[u])のモル質量は35.5[g]
9Be(質量数9,相対原子質量=原子量9.01[u])のモル質量は9.01[g]≒9[g]
物質量 [mol]
物質の質量[g]をモル質量[g/mol]で換算したものです。
ある重さの物質が何モル分あるかを意味します。
24[g]の12Cの物質量は
24[g] ÷ 12[g/mol] = [2mol]
電子密度n
炭素原子(原子量12[u])の密度ρが3.6[g/cm3]のとき、その中に軌道電子がどれくらい含まれるのか計算します。なお、軌道電子の質量は原子量に含めます。
まず、1cm3の中に炭素原子が何個あるか計算します。
1[cm3]の質量は
1[cm3]×3.6[g/cm3]=3.6[g]
$$ ρ $$
です。
炭素原子のモル質量は原子量と同じなので、物質量は
3.6[g]÷12[g/mol]=0.3[mol]
$$ \frac{ρ}{A} $$
です。
1molに含まれる原子数はアボガドロ数NAより6.0×1023[個/mol]なので
0.3[mol]×6.0×1023[個/mol]=1.8×1023[個]
$$ \frac{ρ}{A}・N_A $$
となります。
1個の原子には陽子の数(=原子番号Z)の電子があります。
つまり12Cには6個の電子が存在します。
よって
6[個(電子)/個(原子)]×1.8×1023[個(原子)]=10.8[個(電子)]
$$ \frac{ρ}{A}・N_A・Z $$
となります。
1cm3あたりの電子数は次の式で表されます。
$$ n=\frac{ρ}{A}・N_A・Z $$


コメント